
題目列表(包括答案和解析)
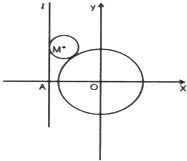 已知直線l:x=m(m<-2)與x軸交于A點,動圓M與直線l相切,并且和圓O:x2+y2=4相外切.
已知直線l:x=m(m<-2)與x軸交于A點,動圓M與直線l相切,并且和圓O:x2+y2=4相外切.| π | 3 |
過點 的圓C與直線
的圓C與直線 相切于點
相切于點 .
.
(1)求圓C的方程;
(2)已知點 的坐標為
的坐標為 ,設
,設 分別是直線
分別是直線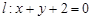 和圓
和圓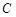 上的動點,求
上的動點,求 的最小值.
的最小值.
(3)在圓C上是否存在兩點 關于直線
關于直線 對稱,且以
對稱,且以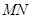 為直徑的圓經過原點?若存在,寫出直線
為直徑的圓經過原點?若存在,寫出直線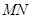 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
過點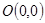 的圓C與直線
的圓C與直線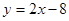 相切于點
相切于點 .
.
(1)求圓C的方程;
(2)已知點 的坐標為
的坐標為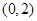 ,設
,設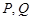 分別是直線
分別是直線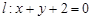 和圓
和圓 上的動點,求
上的動點,求 的最小值.
的最小值.
(3)在圓C上是否存在兩點 關于直線
關于直線 對稱,且以
對稱,且以 為直徑的圓經過原點?若存在,寫出直線
為直徑的圓經過原點?若存在,寫出直線 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
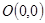 的圓C與直線
的圓C與直線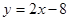 相切于點
相切于點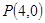 .
.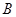 的坐標為
的坐標為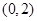 ,設
,設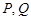 分別是直線
分別是直線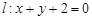 和圓
和圓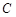 上的動點,求
上的動點,求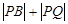 的最小值.
的最小值.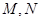 關于直線
關于直線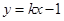 對稱,且以
對稱,且以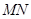 為直徑的圓經過原點?若存在,寫出直線
為直徑的圓經過原點?若存在,寫出直線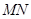 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.已知直線l:x=m(m<-2)與x軸交于A點,動圓M與直線l相切,并且與圓O:x2+y2=4相外切.
(1)求動圓圓心M的軌跡C的方程:
(2)若過原點且傾斜角為![]() 的直線與曲線C交于M、N兩點,問:是否存在以MN為直徑的圓經過點A,若存在,求出m的值;若不存在,說明理由
的直線與曲線C交于M、N兩點,問:是否存在以MN為直徑的圓經過點A,若存在,求出m的值;若不存在,說明理由
一、選擇題 ABCBD DBCDC CC
二、填空題
13.6; ;14.
;14. ;15.
;15. ,1)∪(1,+∞);16。①③④
,1)∪(1,+∞);16。①③④
三、解答題
17. 解:(1)∵  , 且與向量
, 且與向量 所成角為
所成角為
∴  ,
∴
,
∴  ,
,
又 ,∴
,∴
 ,即
,即 。
。
(2)由(1)可得:
∴ 



∵  ,∴
,∴
 ,
,
∴  ,∴
當
,∴
當 =1時,A=
=1時,A=
∴AB=2, 則
18.解:(1)P=
(2)隨機變量 的取值為0, 1, 2, 3.
的取值為0, 1, 2, 3.
由n次獨立重復試驗概率公式 得
得




隨機變量 的分布列是
的分布列是

0
1
2
3





 的數學期望是
的數學期望是 
19.(I)解:取CE中點P,連結FP、BP,
∵F為CD的中點,∴FP//DE,且FP=
又AB//DE,且AB= ,∴AB//FP,且AB=FP,
,∴AB//FP,且AB=FP,
∴ABPF為平行四邊形,∴AF//BP。…………2分
又∵AF 平面BCE,BP
平面BCE,BP 平面BCE,∴AF//平面BCE。
…………4分
平面BCE,∴AF//平面BCE。
…………4分
(II)∵△ACD為正三角形,∴AF⊥CD。
∵AB⊥平面ACD,DE//AB,∴DE⊥平面ACD,又AF 平面ACD,
平面ACD,
∴DE⊥AF。又AF⊥CD,CD∩DE=D,∴AF⊥平面CDE。 …………6分
又BP//AF,∴BP⊥平面CDE。又∵BP 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE。 …………8分
(III)由(II),以F為坐標原點,FA,FD,FP所在的直線分別為x,y,z軸(如圖),建立空間直角坐標系F―xyz.設AC=2,
則C(0,―1,0), ………………9分
………………9分
 ……10分
……10分
顯然, 為平面ACD的法向量。
為平面ACD的法向量。
設平面BCE與平面ACD所成銳二面角為
 ,即平面BCE與平面ACD所成銳二面角為45°。…………12分
,即平面BCE與平面ACD所成銳二面角為45°。…………12分
20.(1)

 時,
時, ,即
,即
當 時,
時,
即
 在
在 上是減函數的充要條件為
上是減函數的充要條件為 ………(4分)
………(4分)
(2)由(1)知,當 時
時 為減函數,
為減函數, 的最大值為
的最大值為 ;
;
當 時,
時,
 當
當 時
時 ,當
,當 時
時
即在 上
上 是增函數,在
是增函數,在 上
上 是減函數,
是減函數, 時
時 取最大值,最大值為
取最大值,最大值為 即
即 …(8分)
…(8分)
(3)在(1)中取 ,即
,即
由(1)知 在
在 上是減函數
上是減函數
 ,即
,即
 ,解得:
,解得: 或
或
故所求不等式的解集為[ ……………(12分)
……………(12分)
21. 解:(1) ,
, ,
,
又 ,∴數列
,∴數列 是首項為
是首項為 ,公比為
,公比為 的等比數列.
的等比數列.
(2)依(Ⅰ)的結論有 ,即
,即 .
.
 .
.
 .
.
(3) ,又由(Ⅱ)有
,又由(Ⅱ)有
 .
.
則
 (
(  ) =
) = 
=( 1- )<∴ 對任意的
)<∴ 對任意的 ,
, .
.
22.解:(I)由條件知: ………2分
………2分
得 ………4分
………4分
(II)依條件有: ………5分, 由
………5分, 由

 8分
8分

由 ,
, ………10分
………10分
由弦長公式得
由

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com