題目列表(包括答案和解析)
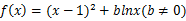
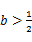時，判斷函數
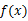在定義域上的單調性。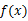有極值點，求b的取值范圍及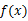的極值點。（09年湖北百所重點聯考文）（13分）
某特許專營店銷售北京奧運會紀念章，每枚進價為5元，同時每銷售一枚這種紀念章還需向北京奧組委交特許經營管理費2元，預計這種紀念章以每枚20元的價格銷售時該店一年可銷售2000枚，經過市場調研發現每枚紀念章的銷售價格在每枚20元的基礎上每減少一元則增加銷售400枚，而每增加一元則減少銷售100枚，現設每枚紀念章的銷售價格為x元。
（1）寫出該特許專營店一年內銷售這種紀念章所獲得的利潤y元（y>0）與每枚紀念章的銷售價格
的函數關系式（并寫出這個函數的定義域）；
（本題滿分12分）
已知奇函數
在定義域
上是減函數，滿足f(1-a)+f(1-2a)〈0，求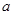
的取值范圍。
（本題滿分12分）
已知奇函數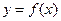
在定義域
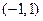上是減函數，滿足f(1-a)+f(1-
2a)〈0，求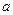
的取值范圍。
（本題滿分14分）
設函數
對于
都有
，且
時，
，
。
（1）說明函數是奇函數還是偶函數？
（2）探究在[-3，3]上是否有最值？若有，請求出最值，若沒有，說明理由；
（3）若的定義域是[-2，2]，解不等式：
一、選擇題（每小題5分，滿分60分）
1
2
3
4
5
6
7
8
9
10
11
12
D
C
D
B
B
A
C
C
A
D
A
D
二、填空題（每小題4分，滿分16分）
13．-6 14．
15．
16．②③
三、解答題（第17、18、19、20、21題各12分，第22題14分，共74分）
17．（I）
（Ⅱ）
函數
的值域為
18．解：（I）記“甲回答對這道題”、“乙回答對這道題”、“丙回答對這道題”分別為事件
、
、
，則
，且有
即
（Ⅱ）由（1）
則甲、乙、丙三人中恰有兩人回答對該題的概率為：
19．解：法一
（I）設
是
的中點，連結
，
則四邊形
為方形，
，故
，
即
又
平面
（Ⅱ）由（I）知
平面，
又
平面，
，
取
的中點
，連結
又
，
則
，取
的中點
，連結
則
為二面角
的平面角
連結
，在
中，
，
取
的中點
，連結
，
，在
中，
二面角的余弦值為
法二：
（I）以
為原點，
所在直線分別為
軸，
軸，
軸建立如圖所示的空間直角坐標系，則
又因為
所以，平面
（Ⅱ）設
為平面
的一個法向量。
由
得
取
，則
又
，
設
為平面
的一個法向量，由
，
，
得
取
取
設
與
的夾角為
，二面角為
，顯然為銳角，
，即為所求
20．解：（I）
或
故
的單調遞增區間是
和
單調遞減區間是（0，2）
（Ⅱ）
在
和
遞增，在（-1，3）遞減。
有三個相異實根
21．解：（I）設
的公差為
，則：
（Ⅱ）當
時，
，由
，得
當
時，
，
，即
是以
為首項，
為公比的等比數列。
（Ⅲ）由（Ⅱ）可知：
22．解：（I）設過
與拋物線
的相切的直線的斜率是
，
則該切線的方程為：
由
得
則
都是方程
的解，故
（Ⅱ）設
由于
，故切線
的方程是：
則
，同理
則直線
的方程是
，則直線過定點（0，2）
（Ⅲ）要使
最小，就是使得到直線的距離最小，而到直線的距離
當且僅當
即
時取等號
設
由
得
，則
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com