
題目列表(包括答案和解析)
(本題滿分12分)
為考察某種甲型H1N1疫苗的效果,進行動物實驗,得到如下疫苗效果的實驗列聯表:
|
|
感染 |
未感染 |
總計 |
|
沒服用 |
20 |
30 |
50 |
|
服用 |
x |
y |
50 |
|
總計 |
M |
N |
100 |
設從沒服用疫苗的動物中任取兩只,感染數為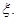 從服從過疫苗的動物中任取兩只,感染數為
從服從過疫苗的動物中任取兩只,感染數為 工作人員曾計算過
工作人員曾計算過
(1)求出列聯表中數據 的值;
的值;
(2)寫出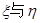 的均值(不要求計算過程),并比較大小,請解釋所得出的結論的實際意義;
的均值(不要求計算過程),并比較大小,請解釋所得出的結論的實際意義;
(3)能夠以97.5%的把握認為這種甲型H1N1疫苗有效么?并說明理由。
參考公式:
參考數據:
|
|
0.05 |
0.025 |
0.010 |
|
|
3.841 |
5.024 |
6.635 |
(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
設二次函數![]() ,對任意實數
,對任意實數![]() ,
,![]() 恒成立;數列
恒成立;數列![]() 滿足
滿足![]() .
.
(1)求函數![]() 的解析式和值域;
的解析式和值域;
(2)試寫出一個區間![]() ,使得當
,使得當![]() 時,數列
時,數列![]() 在這個區間上是遞增數列,
在這個區間上是遞增數列,
并說明理由;
(3)已知![]() ,求:
,求: .
.
.(本題滿分18分)
本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
設二次函數 ,對任意實數
,對任意實數 ,有
,有 恒成立;數列
恒成立;數列 滿足
滿足 .
.
(1)求函數 的解析式和值域;
的解析式和值域;
(2)試寫出一個區間 ,使得當
,使得當 時,數列
時,數列 在這個區間上是遞增數列,
在這個區間上是遞增數列,
并說明理由;
(3)已知 ,是否存在非零整數
,是否存在非零整數 ,使得對任意
,使得對任意 ,都有
,都有

 恒成立,若存在,
恒成立,若存在,
求之;若不存在,說明理由.
 ,對任意實數
,對任意實數 ,有
,有 恒成立;數列
恒成立;數列 滿足
滿足 .
.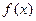 的解析式和值域;
的解析式和值域; ,使得當
,使得當 時,數列
時,數列 在這個區間上是遞增數列,
在這個區間上是遞增數列, ,是否存在非零整數
,是否存在非零整數 ,使得對任意
,使得對任意 ,都有
,都有

 恒成立,若存在,
恒成立,若存在,已知函數 在
在 取得極值
取得極值
(1)求 的單調區間(用
的單調區間(用 表示);
表示);
(2)設 ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范圍.
的取值范圍.
【解析】第一問利用

根據題意 在
在 取得極值,
取得極值, 
對參數a分情況討論,可知
當 即
即 時遞增區間:
時遞增區間:  遞減區間:
遞減區間:  ,
,

當 即
即 時遞增區間:
時遞增區間:  遞減區間:
遞減區間:  ,
,

第二問中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


從而求解。
解: 
 …..3分
…..3分
 在
在 取得極值,
取得極值,  ……………………..4分
……………………..4分
(1) 當 即
即 時 遞增區間:
時 遞增區間:  遞減區間:
遞減區間:  ,
,

當 即
即 時遞增區間:
時遞增區間:  遞減區間:
遞減區間:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com