
題目列表(包括答案和解析)
已知集合![]() ,則
,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知集合![]() ,則
,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
.已知集合![]() ,則
,則![]() =( )
=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
已知集合![]() ,則
,則![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知集合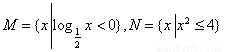 ,則
,則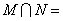 ( )
( )
A. 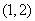 B.
B. 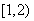 C.
C. 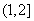 D.
D. 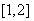
一、選擇題
1
2
3
4
5
6
7
8
9
10
11
12
B
C
A
B
D
A
D
B
A
C
D
C
1、B
解: -
- =
= ,
, -
- =
= ,
, <
< ,故(A)錯。
,故(A)錯。
( +
+ )2=8+2
)2=8+2 ,(
,( +
+ )2=8+2
)2=8+2 ,故(B)對。
,故(B)對。
( +
+ )2=20+
)2=20+ ,(3+
,(3+ )2=20+
)2=20+ ,故(C)錯。
,故(C)錯。
5+ <5+
<5+ =8,故(D)也錯。
=8,故(D)也錯。
2、C
解:由 ,得
,得 ,即,-2<x-1<1,即-1<x<2,又x
,即,-2<x-1<1,即-1<x<2,又x Z,所以x為0,1,即N={0,1},故可選(C)。
Z,所以x為0,1,即N={0,1},故可選(C)。
3、A
解: =-
=- -2<0,故①錯;
-2<0,故①錯;
 =
= ≥0,故②對;
≥0,故②對;
 =
= ,因為
,因為 ,b符號不確定,故③不一定成立。
,b符號不確定,故③不一定成立。
對于④,因為a,b的符號不確定,也不成立。
4、B
解:當(dāng)a,b都大于0時,由 ,得a≥b,所以,有
,得a≥b,所以,有 成立,
成立,
當(dāng)a,b都小于0時,由 ,得a≤b,所以,有
,得a≤b,所以,有 成立,必要性成立。
成立,必要性成立。
而當(dāng)a<b,且b<0時, 成立,
成立, 不成立,充分性不成立。
不成立,充分性不成立。
5、D
解:當(dāng)x=0時,原不等式為 +4≥0顯然成立,當(dāng)x=2時,原不等式為
+4≥0顯然成立,當(dāng)x=2時,原不等式為 +4≥2
+4≥2 +2,即
+2,即 -2
-2 +2≥0,即(k2-1)2+1≥0,也成立,故選(D)。
+2≥0,即(k2-1)2+1≥0,也成立,故選(D)。
6、A
解:由x(3-x)>0,得x2-3x<0,解得:0<x<3。
7、D
解:由 ,且
,且 ,∴
,∴ ,∴
,∴
 。
。
8、B
解:依題意,有 ,解得:
,解得: ,f(x)=
,f(x)= ,
,
f(-x)= ,開口向下,與x軸交點為2,-1,對稱軸為x=
,開口向下,與x軸交點為2,-1,對稱軸為x=
9、A
解:依題意,直線經(jīng)過圓的圓心,圓心為(-1,2),故有-2a-2b+2=0,即a+b=1,

 =
= =
= ≥
≥ =4
=4
10、C
解:如圖知區(qū)域的面積是△OAB去掉一個小直角三角形。
(陰影部分面積比1大,比 小,故選C,不需要算出來)
小,故選C,不需要算出來)
11、D.由題意知直線 與圓
與圓 有交點,則
有交點,則 .
.
另解:設(shè)向量 ,由題意知
,由題意知
由 可得
可得
12、C
解:由 ,可得:
,可得:
知滿足事件A的區(qū)域:的面積 10,而滿足所有條件的區(qū)域
10,而滿足所有條件的區(qū)域 的面積:
的面積: ,從而,得:
,從而,得: 。
。
二、填空題
13、
解:A= ,B=
,B= ,可求
,可求 。
。
14、3
 解:由
解:由 得
得 ,代入
,代入 得
得 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng) =3
=3 時取“=”.
時取“=”.
15、5
解:如圖,由圖象可知目標(biāo)函數(shù) 過點
過點 時
時
 取得最大值,
取得最大值, ,
,
16、a≤0.
解:a≤ 在[1,2]上恒成立,a≤(
在[1,2]上恒成立,a≤( )min=(
)min=( )min=0.
)min=0.
三、解答題
17、解:(I)由 ,得
,得 .
.
(II) .
.
由 ,得
,得 ,又
,又 ,所以
,所以 ,
,
即 的取值范圍是
的取值范圍是 .
.
18.解:(Ⅰ)由題意得:


(Ⅱ)設(shè)框架用料長度為 ,
,
則


當(dāng)且僅當(dāng)
 滿足
滿足
答:當(dāng)  米,
米, 米時,用料最少.
米時,用料最少.
19、解:(1)依題意三角形NDC與三角形NAM相似,
所以 ,即
,即 ,
,  ,
,
矩形ABCD的面積為 ,定義域為
,定義域為 ,
,
要使倉庫占地ABCD的面積不少于144平方米即 ,
,
化簡得 ,解得
,解得 所以AB長度應(yīng)在
所以AB長度應(yīng)在 內(nèi).
內(nèi).
(2)倉庫體積為
 得
得 ,
,
當(dāng) 時
時 ,當(dāng)
,當(dāng) 時
時 所以
所以 時V取最大值
時V取最大值 米3,
米3,
即AB長度為20米時倉庫的庫容最大.
20、解:(1)
即 (
( );
);
(2)由均值不等式得:
 (萬元)
(萬元)
當(dāng)且僅當(dāng) ,即
,即 時取到等號.
時取到等號.
答:該企業(yè)10年后需要重新更換新設(shè)備.
21、設(shè)
 ,
,


 =
=
因為 是
是 的必要不充分條件,所以
的必要不充分條件,所以

 ,且
,且 推不出
推不出
而 ,
,
所以 ,則
,則
即
22、解:設(shè)
連結(jié)BD.
則在 中,
中,


設(shè)
則
等號成立時
答:當(dāng) 時,建造這個支架的成本最低.
時,建造這個支架的成本最低.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com