
題目列表(包括答案和解析)
函數(shù) 在同一個(gè)周期內(nèi),當(dāng)
在同一個(gè)周期內(nèi),當(dāng) 時(shí),
時(shí), 取最大值1,當(dāng)
取最大值1,當(dāng) 時(shí),
時(shí), 取最小值
取最小值 。
。
(1)求函數(shù)的解析式
(2)函數(shù) 的圖象經(jīng)過(guò)怎樣的變換可得到
的圖象經(jīng)過(guò)怎樣的變換可得到 的圖象?
的圖象?
(3)若函數(shù) 滿足方程
滿足方程 求在
求在 內(nèi)的所有實(shí)數(shù)根之和.
內(nèi)的所有實(shí)數(shù)根之和.
【解析】第一問(wèn)中利用
又因
又
 函數(shù)
函數(shù)
第二問(wèn)中,利用 的圖象向右平移
的圖象向右平移 個(gè)單位得
個(gè)單位得 的圖象
的圖象
再由 圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的 .縱坐標(biāo)不變,得到
.縱坐標(biāo)不變,得到 的圖象,
的圖象,
第三問(wèn)中,利用三角函數(shù)的對(duì)稱(chēng)性, 的周期為
的周期為
 在
在 內(nèi)恰有3個(gè)周期,
內(nèi)恰有3個(gè)周期,
并且方程 在
在 內(nèi)有6個(gè)實(shí)根且
內(nèi)有6個(gè)實(shí)根且
同理, 可得結(jié)論。
可得結(jié)論。
解:(1)
又因
又
 函數(shù)
函數(shù)
(2) 的圖象向右平移
的圖象向右平移 個(gè)單位得
個(gè)單位得 的圖象
的圖象
再由 圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的 .縱坐標(biāo)不變,得到
.縱坐標(biāo)不變,得到 的圖象,
的圖象,
(3) 的周期為
的周期為
 在
在 內(nèi)恰有3個(gè)周期,
內(nèi)恰有3個(gè)周期,
并且方程 在
在 內(nèi)有6個(gè)實(shí)根且
內(nèi)有6個(gè)實(shí)根且
同理,
故所有實(shí)數(shù)之和為
 個(gè)單位得y=cosx的圖象
個(gè)單位得y=cosx的圖象 個(gè)單位得y=sinx的圖象
個(gè)單位得y=sinx的圖象 的圖象向右平移
的圖象向右平移 個(gè)單位得函數(shù)g(x)的圖象,再將g(x)的圖象所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍得到函數(shù)h(x)的圖象,則( )
個(gè)單位得函數(shù)g(x)的圖象,再將g(x)的圖象所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍得到函數(shù)h(x)的圖象,則( )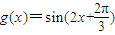 ,
,
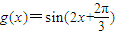 ,
,
 的圖象向右平移
的圖象向右平移 個(gè)單位得函數(shù)g(x)的圖象,再將g(x)的圖象所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍得到函數(shù)h(x)的圖象,則
個(gè)單位得函數(shù)g(x)的圖象,再將g(x)的圖象所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍得到函數(shù)h(x)的圖象,則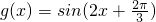 ,
,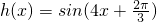
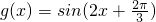 ,
,
(本小題滿分12分)若函數(shù) 在區(qū)間[
在區(qū)間[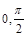 ]上的最大值為6,
]上的最大值為6,
(1)求常數(shù)m的值
(2)作函數(shù)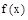 關(guān)于y軸的對(duì)稱(chēng)圖象得函數(shù)
關(guān)于y軸的對(duì)稱(chēng)圖象得函數(shù)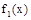 的圖象,再把
的圖象,再把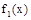 的圖象向右平移
的圖象向右平移 個(gè)單位得
個(gè)單位得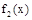 的圖象,求函數(shù)
的圖象,求函數(shù)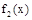 的單調(diào)遞減區(qū)間.
的單調(diào)遞減區(qū)間.
一、選擇題:
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
A
D
C
A
D
C
B
D
B
C
二、填空題:
13、 14、
14、 15、
15、 等; 16、7
等; 16、7
三、解答題
17、(1)由余弦定理: 又
又
∴ ∴
∴
(2)∵A+B+C= ∴
∴
∴
18、(1) (2)
(2)
19、(1)AC=1,BC=2 ,AB= ,∴
,∴ ∴AC
∴AC
又 平面PAC 平面ABC,平面PAC
平面ABC,平面PAC 平面ABC=AC,∴BC
平面ABC=AC,∴BC 平面PAC
平面PAC
又∵PA 平面APC ∴
平面APC ∴
 (2)該幾何體的主試圖如下:
(2)該幾何體的主試圖如下:
幾何體主試圖的面積為
 ∴
∴ ∴
∴
(3)取PC 的中點(diǎn)N,連接AN,由△PAC是邊長(zhǎng)為1的正三角形,可知
由(1)BC 平面PAC,可知
平面PAC,可知 ∴
∴ 平面PCBM
平面PCBM
∴
20、(1) 的最小值為
的最小值為
(2)a的取值范圍是
21、(1)曲線C的方程為
(2) ,存在點(diǎn)M(―1,2)滿足題意
,存在點(diǎn)M(―1,2)滿足題意
22、(1)由于點(diǎn)B1(1,y1),B2(2,y2),…,Bn(n,yn)( )在直線
)在直線 上
上
則 因此
因此 ,所以
,所以 是等差數(shù)列
是等差數(shù)列
(2)由已知有 得
得 同理
同理 
∴
∴

∴
(3)由(2)得 ,則
,則

∴
∴
∴
由于 而
而
則
 ,從而
,從而
同理: ……
…… 
以上 個(gè)不等式相加得:
個(gè)不等式相加得:
即 ,從而
,從而

國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com