
題目列表(包括答案和解析)
在 中,滿足
中,滿足 ,
, 是
是 邊上的一點.
邊上的一點.
(Ⅰ)若 ,求向量
,求向量 與向量
與向量 夾角的正弦值;
夾角的正弦值;
(Ⅱ)若 ,
, =m (m為正常數) 且
=m (m為正常數) 且 是
是 邊上的三等分點.,求
邊上的三等分點.,求 值;
值;
(Ⅲ)若 且
且 求
求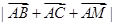 的最小值。
的最小值。
【解析】第一問中,利用向量的數量積設向量 與向量
與向量 的夾角為
的夾角為 ,則
,則
令 =
= ,得
,得 ,又
,又 ,則
,則 為所求
為所求
第二問因為 ,
, =m所以
=m所以 ,
,
(1)當 時,則
時,則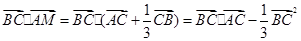 =
=
(2)當 時,則
時,則 =
=
第三問中,解:設 ,因為
,因為
 ,
, ;
;
所以 即
即 于是
于是 得
得
從而
運用三角函數求解。
(Ⅰ)解:設向量 與向量
與向量 的夾角為
的夾角為 ,則
,則
令 =
= ,得
,得 ,又
,又 ,則
,則 為所求……………2分
為所求……………2分
(Ⅱ)解:因為 ,
, =m所以
=m所以 ,
,
(1)當 時,則
時,則 =
= ;-2分
;-2分
(2)當 時,則
時,則 =
= ;--2分
;--2分
(Ⅲ)解:設 ,因為
,因為
 ,
, ;
;
所以 即
即 于是
于是 得
得
從而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令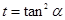 ,
, 則
則 ,則函數
,則函數 ,在
,在 遞減,在
遞減,在 上遞增,所以
上遞增,所以 從而當
從而當 時,
時,
| a+2 |
| 2 |
| 2+2 |
| 2 |
| a+2 |
| 2 |
| a+a |
| 2 |
| n |
| m |
| n0 |
| m0 |
| n0+1 |
| m0+1 |
| n0+1 |
| m0+1 |
已知二次函數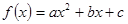
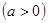 ,方程
,方程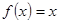 的兩個根為
的兩個根為 ,
,
滿足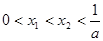 ,那么當
,那么當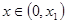 時,
時, 與
與 的大小關系為(
)
的大小關系為(
)
A 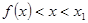 B
B
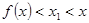 C
C
 D
D

在解決問題:“證明數集 沒有最小數”時,可用反證法證明.
沒有最小數”時,可用反證法證明.
假設 是
是 中的最小數,則取
中的最小數,則取 ,可得:
,可得: ,與假設中“
,與假設中“ 是
是 中的最小數”矛盾! 那么對于問題:“證明數集
中的最小數”矛盾! 那么對于問題:“證明數集 沒有最大數”,也可以用反證法證明.我們可以假設
沒有最大數”,也可以用反證法證明.我們可以假設 是
是 中的最大數,則可以找到
中的最大數,則可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知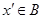 ,
, ,這與假設矛盾!所以數集
,這與假設矛盾!所以數集 沒有最大數.
沒有最大數.
下列敘述中正確的是( )
①反證法原理是在假設 下,如果推出一個矛盾,就證明
下,如果推出一個矛盾,就證明 不成立.
不成立.
②獨立性檢驗原理是在假設 下,如果出現一個與
下,如果出現一個與 相矛盾的小概率事件,就推斷
相矛盾的小概率事件,就推斷 不成立,且該推斷犯錯誤的概率不超過這個小概率.
不成立,且該推斷犯錯誤的概率不超過這個小概率.
③三段論可以表示為:大前提:M是P.小前提:S是M.結 論:S是P.
④流程圖常常用來表示一些動態過程,通常會有一個 “起點”,一個或多個“終點”.程序框圖是流程圖的一種.
A.①②③ B.①②④ C.②③④ D.①②③④
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com