
題目列表(包括答案和解析)
有甲、乙兩個班級進行數學考試,按照大于或等于85分為優秀,85分以下為非優秀統計成績后,得到如下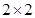 聯表:
聯表:
|
|
優秀 |
非優秀 |
合計 |
|
甲班 |
30 |
|
|
|
乙班 |
|
50 |
|
|
合計 |
|
|
200 |
已知全部200人中隨機抽取1人為優秀的概率為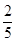
(1)請完成上面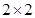 聯表;
聯表;
(2)根據列聯表的數據,能否有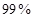 的把握認為“成績與班級有關系”
的把握認為“成績與班級有關系”
(3)從全部200人中有放回抽取3次,每次抽取一人,記被抽取的3人中優秀的人數為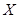 ,若每次抽取得結果是相互獨立的,求
,若每次抽取得結果是相互獨立的,求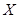 的分布列,期望
的分布列,期望 和方差
和方差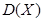
參考公式與參考數據如下:
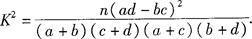
有甲、乙兩個班級進行數學考試,按照大于或等于85分為優秀,85分以下為非優秀統計成績后,得到如下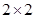 聯表:
聯表:
| | 優秀 | 非優秀 | 合計 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合計 | | | 200 |
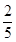
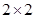 聯表;
聯表;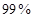 的把握認為“成績與班級有關系”
的把握認為“成績與班級有關系” ,若每次抽取得結果是相互獨立的,求
,若每次抽取得結果是相互獨立的,求 的分布列,期望
的分布列,期望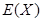 和方差
和方差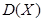

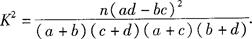
 聯表:
聯表:| | 優秀 | 非優秀 | 合計 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合計 | | | 200 |

 聯表;
聯表; 的把握認為“成績與班級有關系”
的把握認為“成績與班級有關系” ,若每次抽取得結果是相互獨立的,求
,若每次抽取得結果是相互獨立的,求 的分布列,期望
的分布列,期望 和方差
和方差


某中學研究性學習小組,為了考察高中學生的作文水平與愛看課外書的關系,在本校高三年級隨機調查了 50名學生.調査結果表明:在愛看課外書的25人中有18人作文水平好,另7人作文水平一般;在不愛看課外書的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)試根據以上數據完成以下2×2列聯表,并運用獨立性檢驗思想,指出有多大把握認為中學生的作文水平與愛看課外書有關系?
高中學生的作文水平與愛看課外書的2×2列聯表
|
|
愛看課外書 |
不愛看課外書 |
總計 |
|
作文水平好 |
|
|
|
|
作文水平一般 |
|
|
|
|
總計 |
|
|
|
(Ⅱ)將其中某5名愛看課外書且作文水平好的學生分別編號為1、2、3、4、5,某5名愛看課外書且作文水平一般的學生也分別編號為1、2、3、4、5,從這兩組學生中各任選1人進行學習交流,求被選取的兩名學生的編號之和為3的倍數或4的倍數的概率.
參考公式: ,其中
,其中 .
.
參考數據:
|
|
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
【解析】本試題主要考查了古典概型和列聯表中獨立性檢驗的運用。結合公式為 判定兩個分類變量的相關性,
判定兩個分類變量的相關性,
第二問中,確定
結合互斥事件的概率求解得到。
解:因為2×2列聯表如下
|
|
愛看課外書 |
不愛看課外書 |
總計 |
|
作文水平好 |
18 |
6 |
24 |
|
作文水平一般 |
7 |
19 |
26 |
|
總計 |
25 |
25 |
50 |

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com