
題目列表(包括答案和解析)
(本小題滿分12分)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
,
![]() ;(1)求數列
;(1)求數列![]() 的通項公式
的通項公式
(2)設數列![]() 滿足:
滿足:![]() ,且
,且![]() ,求證:
,求證:![]() (3)若(2)問中數列
(3)若(2)問中數列![]() 滿足
滿足 ![]() ,
,
求證: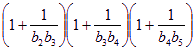
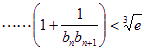 (其中
(其中![]() 為自然對數的底數)。
為自然對數的底數)。
(本小題滿分12分)
為了解某班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
|
|
喜愛打籃球 |
不喜愛打籃球 |
合計 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
[來源:學|科|網] |
|
合計 |
|
|
50[] |
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為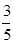
(1)請將上面的列聯表補充完整
(2)是否有99.5%的把握認為喜愛打籃球與性別有關?說明你的理由;
(3)已知喜愛打籃球的10位女生中, 還喜歡打羽毛球,
還喜歡打羽毛球,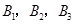
還喜歡打乒乓球,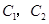 還喜歡踢足球,現在從喜歡打羽毛球、喜歡打乒乓球、
還喜歡踢足球,現在從喜歡打羽毛球、喜歡打乒乓球、
喜歡踢足球的8位女生中各選出1名進行其他方面的調查,求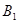 和
和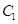 不全被選
不全被選
中的概率.
下面的臨界值表供參考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小題滿分12分)某校高一(2)班共有60名同學參加期末考試,現將其數學學科成績(均為整數)分成六個分數段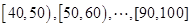 ,畫出如下圖所示的部分頻率分布直方圖,請觀察圖形信息,回答下列問題:
,畫出如下圖所示的部分頻率分布直方圖,請觀察圖形信息,回答下列問題:
(1)求70~80分數段的學生人數;
(2)估計這次考試中該學科的優分率(80分及以上為優分)
(3)現根據本次考試分數分成下列六段(從低分段到高分段依次為第一組、第二組、…、第六組)為提高本班數學整體成績,決定組與組之間進行幫扶學習.若選出的兩組分數之差大于30分(以分數段為依據,不以具體學生分數為依據),則稱這兩組為“最佳組合”,試求選出的兩組為“最佳組合”的概率.[來源:學#科#網]
(本小題滿分12分)
道路交通安全法中將飲酒后違法駕駛機動車的行為分成兩個檔次:“酒后駕車”和“醉酒駕車”,其檢測標準是駕駛人員血液中的酒精含量Q(簡稱血酒含量,單位是毫克/100毫升),當20≤Q<80時,為酒后駕車;當Q≥80時,為醉酒駕車. 某市公安局交通管理部門在某路段的一次攔查行動中,依法檢查了200輛機動車駕駛員的血酒含量,其中查處酒后駕車的有6人,查處醉酒駕車的有2人,依據上述材料回答下列問題:
(1)分別寫出違法駕車發生的頻率和醉酒駕車占違法駕車總數的百分數;
(2)從違法駕車的8人中抽取2人,求取到醉酒駕車人數的分布列和期望,并指出所求期望的實際意義;
(3)飲酒后違法駕駛機動車極易發生交通事故,假設酒后駕車和醉酒駕車發生交通事故的概率分別是0.1和0.25,且每位駕駛員是否發生交通事故是相互獨立的。依此計算被查處的8名駕駛員中至少有一人發生交通事故的概率。(精確到0.01)并針對你的計算結果對駕駛員發出一句話的倡議.
(本小題滿分12分)
2011年4月28日,世界園藝博覽會已在西安正式開園,正式開園前,主辦方安排了4次試運行,為了解前期準備情況和試運行中出現的問題,以做改進,組委會組織了一次座談會,共邀請20名代表參加,他們分別是游客15人,志愿者5人。
(I)從這20名代表中隨機選出3名談建議,求至少有1人是志愿者的概率;
(II)若隨機選出2名代表發言,![]() 表示其游客人數,求
表示其游客人數,求![]() 的分布列和數學期望。
的分布列和數學期望。
一、DDBCD CABCA
二、11.1;
12. ; 13.
; 13. 14.
14. ; 15.
; 15. ;
;
16.
三.解答題(本大題共6小題,共76分)
17.解:(1)法一:由題可得 ;
;
法二:由題 ,
,
故 ,從而
,從而 ;
;
法三:由題 ,解得
,解得 ,
,
故 ,從而
,從而 。
。
(2) ,令
,令 ,
,
則 ,
,
 在
在 單調遞減,
單調遞減,
故
 ,
,
從而 的值域為
的值域為 。
。
18.解:(1) 的可能取值為0,1,2,3,4,
的可能取值為0,1,2,3,4, ,
,

 ,
,
 ,
, ,
,
 。
。
因此隨機變量 的分布列為下表所示;
的分布列為下表所示;

0
1
2
3
4






(2)由⑴得: ,
,

19.法一:(1)連接 ,設
,設 ,則
,則 。
。
因為 ,所以
,所以 ,故
,故 ,從而
,從而 ,
,
故 。
。
又因為 ,
,
所以 ,當且僅當
,當且僅當 取等號。
取等號。
此時 為
為 邊的中點,
邊的中點, 為
為 邊的中點。
邊的中點。
故當 為
為 邊的中點時,
邊的中點時, 的長度最小,其值為
的長度最小,其值為
(2)連接 ,因為此時
,因為此時 分別為
分別為 的中點,
的中點,
故 ,所以
,所以 均為直角三角形,
均為直角三角形,
從而 ,所以
,所以 即為直線
即為直線 與平面
與平面 所成的角。
所成的角。
因為 ,所以
,所以 即為所求;
即為所求;
(3)因 ,又
,又 ,所以
,所以 。
。
又 ,故三棱錐
,故三棱錐 的表面積為
的表面積為
 。
。
因為三棱錐 的體積
的體積 ,
,
所以 。
。
法二:(1)因 ,故
,故 。
。
設 ,則
,則 。
。
所以 ,
,
當且僅當 取等號。此時
取等號。此時 為
為 邊的中點。
邊的中點。
故當 為
為 的中點時,
的中點時, 的長度最小,其值為
的長度最小,其值為 ;
;
(2)因 ,又
,又 ,所以
,所以 。
。
記 點到平面
點到平面 的距離為
的距離為 ,
,
因 ,故
,故 ,解得
,解得 。
。
 因
因 ,故
,故 ;
;
(3)同“法一”。
法三:(1)如圖,以 為原點建立空間直角坐標系,設
為原點建立空間直角坐標系,設 ,則
,則 ,
,
所以 ,當且僅當
,當且僅當 取等號。
取等號。
此時 為
為 邊的中點,
邊的中點, 為
為 邊的中點。
邊的中點。
故當 為
為 邊的中點時,
邊的中點時, 的長度最小,其值為
的長度最小,其值為 ;
;
(2)設 為面
為面 的法向量,因
的法向量,因 ,
,
故 。取
。取 ,得
,得 。
。
又因 ,故
,故 。
。
因此 ,從而
,從而 ,
,
所以 ;
;
(3)由題意可設 為三棱錐
為三棱錐 的內切球球心,
的內切球球心,
則 ,可得
,可得 。
。
與(2)同法可得平面 的一個法向量
的一個法向量 ,
,
又 ,故
,故 ,
,
解得 。顯然
。顯然 ,故
,故 。
。
20.解:(1)當 時,
時, 。令
。令 得
得 ,
,
故當 時
時 ,
, 單調遞增;
單調遞增;
當 時
時 ,
, 單調遞減。
單調遞減。
所以函數 的單調遞增區間為
的單調遞增區間為 ,
,
單調遞減區間為 ;
;
(2)法一:因 ,故
,故 。
。
令 ,
,
要使 對滿足
對滿足 的一切
的一切 成立,則
成立,則 ,
,
解得 ;
;
法二: ,故
,故 。
。
由 可解得
可解得 。
。
因為 在
在 單調遞減,因此
單調遞減,因此 在
在 單調遞增,故
單調遞增,故 。設
。設 ,
,
則 ,因為
,因為 ,
,
所以 ,從而
,從而 在
在 單調遞減,
單調遞減,
故 。因此
。因此 ,即
,即 。
。
(3)因為 ,所以
,所以
即 對一切
對一切 恒成立。
恒成立。
 ,令
,令 ,
,
則 。因為
。因為 ,所以
,所以 ,
,
故 在
在 單調遞增,有
單調遞增,有 。
。
因此 ,從而
,從而 。
。
所以 。
。
21.解:(1)設 ,則由題
,則由題 ,
,
由 得
得 ,故
,故 。
。
又根據 可得
可得 ,
,
即 ,代入可得
,代入可得 ,
,
解得 (舍負)。故
(舍負)。故 的方程為
的方程為 ;
;
(2)法一:設 ,代入
,代入 得
得 ,
,
故 ,
,
從而


因此 。
。
法二:顯然點 是拋物線
是拋物線 的焦點,點
的焦點,點 是其準線
是其準線 上一點。
上一點。
設 為
為 的中點,過
的中點,過 分別作
分別作 的垂線,垂足分別為
的垂線,垂足分別為 ,
,
則 。
。
因此以 為直徑的圓與準線
為直徑的圓與準線 相切(于點
相切(于點 )。
)。
若 與
與 重合,則
重合,則 。否則點
。否則點 在
在 外,因此
外,因此 。
。
綜上知 。
。
22.證明:(1)因 ,故
,故 。
。
顯然 ,因此數列
,因此數列 是以
是以 為首項,以2為公比的等比數列;
為首項,以2為公比的等比數列;
(2)由⑴知 ,解得
,解得 ;
;
(3)因為

所以 。
。
又
 (當且僅當
(當且僅當 時取等號),
時取等號),
故 。
。
綜上可得 。(亦可用數學歸納法)
。(亦可用數學歸納法)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com