
題目列表(包括答案和解析)
(12分)如圖,正四棱錐P![]() ABCD的底面邊長與側(cè)棱長都是2,點O為底面ABCD的中心,M為PC的中點.
ABCD的底面邊長與側(cè)棱長都是2,點O為底面ABCD的中心,M為PC的中點.
(Ⅰ)求異面直線BM和AD所成角的大小;
(Ⅱ)求二面角M![]() PB
PB![]() D的余弦值.
D的余弦值.

 如圖,矩形ABCD與矩形AB′C′D全等,且所在平面所成的二面角為a,記兩個矩形對角線的交點分別為Q,Q′,AB=a,AD=b.
如圖,矩形ABCD與矩形AB′C′D全等,且所在平面所成的二面角為a,記兩個矩形對角線的交點分別為Q,Q′,AB=a,AD=b.| 2 |
| π |
| 3 |
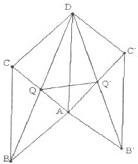
(12分)已知直三棱柱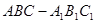 中,
中,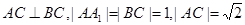 ,點M是
,點M是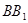 的中點,Q是AB的中點,
的中點,Q是AB的中點,
(1)若P是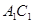 上的一動點,求證:
上的一動點,求證: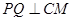 ;
;
(2)求二面角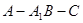 大小的余弦值.
大小的余弦值.

(本小題滿分14分)
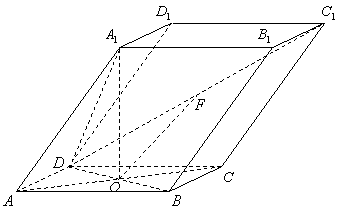
如圖,棱柱ABCD—![]() 的所有棱長都為2,
的所有棱長都為2, ![]() ,側(cè)棱
,側(cè)棱![]() 與底面ABCD的所成角為60°,
與底面ABCD的所成角為60°,![]() ⊥平面ABCD,
⊥平面ABCD,![]() 為
為![]() 的中點.
的中點.
(Ⅰ)證明:BD⊥![]() ;
;
(Ⅱ)證明:![]() 平面
平面![]() ;
;
 (Ⅲ)求二面角D
(Ⅲ)求二面角D![]()
![]()
![]() C的余弦值.
C的余弦值.
(本小題滿分14分)
如圖,棱柱ABCD—![]() 的所有棱長都為2,
的所有棱長都為2, ![]() ,側(cè)棱
,側(cè)棱![]() 與底面ABCD的所成角為60°,
與底面ABCD的所成角為60°,![]() ⊥平面ABCD,
⊥平面ABCD,![]() 為
為![]() 的中點.
的中點.
(Ⅰ)證明:BD⊥![]() ;
;
(Ⅱ)證明:![]() 平面
平面![]() ;
;
 (Ⅲ)求二面角D
(Ⅲ)求二面角D![]()
![]()
![]() C的余弦值.
C的余弦值.
一、選擇題(每小題5分,共50分)
1.B 2.C 3.A 4.D 5.C 6.D 7.B 8.C 9.A 10.D
二、填空題(每小題4分,共24分)
l 1.192 12.286 13. 14.
14. 15.
15.
三、解答題(本大題共6小題,共76分)
17.(本題12分)
解:(Ⅰ)
 ………………………………(2分)
………………………………(2分)

 …………(4分)
…………(4分)

 …………………………………(6分)
…………………………………(6分)
(Ⅱ)
 .
……………(8分)
.
……………(8分)
由已知條件
根據(jù)正弦定理,得 …………………(10分)
…………………(10分)
 ……………………(12分)
……………………(12分)
18.(本題12分)
解:(Ⅰ)在7人中選出3人,總的結(jié)果數(shù)是 種
………………(2分)
種
………………(2分)
記“被選中的3人中至多有1名女生”為事件A,則A包含兩種情形:
①被選中的是1名女生,2名男生的結(jié)果數(shù)是 種,
種,
②被選中的是3名男生的結(jié)果數(shù)是 種,
………………(4分)
種,
………………(4分)
 至多選中1名女生的概率為
至多選中1名女生的概率為 . ……………(6分)
. ……………(6分)
(Ⅱ)由題意知隨機變量 可能的取值為:0,1,2,3,則有
可能的取值為:0,1,2,3,則有

 ……………………(8分)
……………………(8分)
 的分布列
的分布列

0
1
2
3
P




……………(10分)
 的數(shù)學(xué)期望
的數(shù)學(xué)期望 …
……(12分)
…
……(12分)
19.(本題12分)
解:(Ⅰ)連接 ,以
,以 所在的直線為
所在的直線為 軸,
軸, 軸,
軸, 軸
軸
建立如圖所示的空間直角坐標(biāo)系. …………………………………(2分)
 正四棱錐的底面邊長和側(cè)棱長都是2,
正四棱錐的底面邊長和側(cè)棱長都是2,
 .
.
 .
.

 為
為 的中點.
的中點.
 …………(4分)
…………(4分)
 .
.


 即異面直線
即異面直線 和
和 所成的角為
所成的角為 ………(6分)
………(6分)
(Ⅱ) .
.
 是平面
是平面 的一個法向量. ……………………………(8分)
的一個法向量. ……………………………(8分)
由(Ⅰ)得 .
.
設(shè)平面 的一個法向量為
的一個法向量為 ,
,
則由 ,得
,得 .
.
 ,不妨設(shè)
,不妨設(shè) ,
,
得平面 的一個法向量為
的一個法向量為 .
………………(10分)
.
………………(10分)
 .
.
 二面角
二面角 小于
小于 ,
,
 二面角
二面角 的余弦值為
的余弦值為 .
………………(12分)
.
………………(12分)
20.(本題12分)
解:(Ⅰ)由已知得 ,又
,又 ,
,
 即
即 . …………………………(2分)
. …………………………(2分)
 ,公差
,公差 .
.
由 ,得 …………………………(4分)
,得 …………………………(4分)

即 .解得
.解得 或
或 (舍去).
(舍去).
 .
…………………………(6分)
.
…………………………(6分)
(Ⅱ)由 得
得
 …………………………(8分)
…………………………(8分)
 …………………………(9分)
…………………………(9分)
 是等差數(shù)列.
是等差數(shù)列.
則
 ………………………(11分)
………………………(11分)
 ……………………(12分)
……………………(12分)
21.(本題14分)
解:(Ⅰ)依題意得
 .
………………………(2分)
.
………………………(2分)
把(1,3)代入 .
.
解得 .
.
 橢圓的方程為
橢圓的方程為 .
………………………(4分)
.
………………………(4分)
(Ⅱ)由(Ⅰ)得 ,設(shè)
,設(shè) ,如圖所示
,如圖所示

 點在橢圓上,
點在橢圓上,
 . ①
. ①
 點異于頂點
點異于頂點 、
、 ,
,
 .
.
由 、
、 、
、 三點共線,可得
三點共線,可得
從而 …………………………(7分)
…………………………(7分)
 ② …………(8分)
② …………(8分)
將①式代入②式化簡得 …………(10分)
…………(10分)

 …………(12分)
…………(12分)
于是 為銳角,
為銳角, 為鈍角.
為鈍角.
 點B在以MN為直徑的圓內(nèi). ……………(14分)
點B在以MN為直徑的圓內(nèi). ……………(14分)
22.(本題14分)
解:(Ⅰ) ,
,
令 ,得
,得 或
或 .
………………(2分)
.
………………(2分)
當(dāng) 時,
時, 在
在 上單調(diào)遞
上單調(diào)遞
當(dāng) 時,
時, 在
在 上單調(diào)遞減,
上單調(diào)遞減,
而 ,
,
 當(dāng)
當(dāng) 時,
時, 的值域是
的值域是 . ……………(4分)
. ……………(4分)
(Ⅱ)設(shè)函數(shù) 在
在 上的值域是A,
上的值域是A,
 若對任意
若對任意 .總存在
.總存在 1,使
1,使 ,
,
 .
……………(6分)
.
……………(6分)
 .
.
①當(dāng) 時,
時, ,
,
 函數(shù)
函數(shù) 在
在 上單調(diào)遞減.
上單調(diào)遞減.
 ,
,
 當(dāng)
當(dāng) 時,不滿足
時,不滿足 ; ……………………(8分)
; ……………………(8分)
②當(dāng) 時,
時, ,
,
令 ,得
,得 或
或 (舍去 ………………(9分)
(舍去 ………………(9分)
(i) 時,
時, 的變化如下表:
的變化如下表:

0



2

-
0
+

0





 .
.

 ,解得
,解得 . …………………(11分)
. …………………(11分)
(ii)當(dāng) 時,
時,
 函數(shù)
函數(shù) 在
在 上單調(diào)遞減.
上單調(diào)遞減.

 ,
,
 當(dāng)
當(dāng) 時,不滿足
時,不滿足 .
…………………(13分)
.
…………………(13分)
綜上可知,實數(shù) 的取值范圍是
的取值范圍是 . ……………………(14分)
. ……………………(14分)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com