
題目列表(包括答案和解析)
|
|
本題有(1)、(2)、(3)三個選答題,每題7分,請考生任選2題作答,滿分14分.如果多做,則按所做的前兩題記分.作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中.作
(1)選修4—2:矩陣與變換
若二階矩陣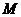 滿足
滿足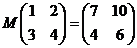 .
.
(Ⅰ)求二階矩陣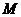 ;
;
(Ⅱ)把矩陣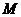 所對應的變換作用在曲線
所對應的變換作用在曲線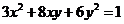 上,求所得曲線的方程.
上,求所得曲線的方程.
(2)選修4-4:坐標系與參數方程
已知在直角坐標系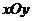 中,曲線
中,曲線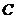 的參數方程為
的參數方程為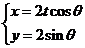 (t為非零常數,
(t為非零常數,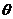 為參數),在極坐標系(與直角坐標系
為參數),在極坐標系(與直角坐標系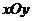 取相同的長度單位,且以原點
取相同的長度單位,且以原點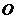 為極點,以
為極點,以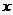 軸正半軸為極軸)中,直線
軸正半軸為極軸)中,直線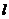 的方程為
的方程為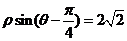 .
.
(Ⅰ)求曲線C的普通方程并說明曲線的形狀;
(Ⅱ)是否存在實數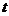 ,使得直線
,使得直線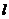 與曲線C有兩個不同的公共點
與曲線C有兩個不同的公共點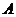 、
、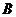 ,且
,且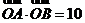 (其中
(其中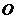 為坐標原點)?若存在,請求出;否則,請說明理由.
為坐標原點)?若存在,請求出;否則,請說明理由.
(3)選修4—5:不等式選講
已知函數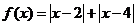 的最小值為
的最小值為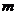 ,實數
,實數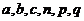 滿足
滿足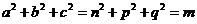 .
.
(Ⅰ)求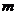 的值;
的值;
(Ⅱ)求證: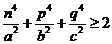 .
.
 ,并且矩陣M對應的變換將點(-1,2)變換成(9,15).求矩陣M.
,并且矩陣M對應的變換將點(-1,2)變換成(9,15).求矩陣M. (α是參數).
(α是參數).
|
|
|
| 2 |
| π |
| 4 |
| x2 |
| 4 |
| y2 |
| 9 |
|
|
| π |
| 3 |
| 4a+1 |
| 4b+1 |
| 4c+1 |
一、填空題
1、--數學.files/image125.gif) 2、40 3、②
④) 4、-1 5、
2、40 3、②
④) 4、-1 5、--數學.files/image127.gif) 6、3
6、3
7、--數學.files/image129.gif) 8、
8、--數學.files/image131.gif) 9、1 10、
9、1 10、--數學.files/image133.gif) 11、
11、--數學.files/image135.gif) 12、46
12、46
13、解:(1)∵a⊥b,∴a?b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a?b=6sin2α+5sinαcosα-4cos2α=0.……………………………………2分
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=---數學.files/image137.gif) ,或tanα=
,或tanα=--數學.files/image139.gif) .……… 6分
.……… 6分
∵α∈(--數學.files/image104.gif) ),tanα<0,故tanα=
),tanα<0,故tanα=--數學.files/image139.gif) (舍去).∴tanα=-
(舍去).∴tanα=---數學.files/image137.gif) .…………7分
.…………7分
(2)∵α∈(--數學.files/image104.gif) ),∴
),∴--數學.files/image141.gif) .
.
由tanα=---數學.files/image137.gif) ,求得
,求得--數學.files/image143.gif) ,
,--數學.files/image145.gif) =2(舍去).
=2(舍去).
∴--數學.files/image147.gif) ,…………………………………………………………12分
,…………………………………………………………12分
cos(--數學.files/image149.gif) )=
)=--數學.files/image151.gif) =
=--數學.files/image153.gif) =
=--數學.files/image155.gif) . ……15分
. ……15分
14、解:由已知圓的方程為--數學.files/image157.gif) ,
,
按--數學.files/image159.gif) 平移得到
平移得到--數學.files/image161.gif) .
.
∵--數學.files/image163.gif) ∴
∴--數學.files/image165.gif) .
.
即--數學.files/image167.gif) .
.
又--數學.files/image169.gif) ,且
,且--數學.files/image159.gif) ,∴
,∴--數學.files/image172.gif) .∴
.∴--數學.files/image174.gif) .
.
設--數學.files/image176.gif) ,
, --數學.files/image178.gif) 的中點為D.
的中點為D.
由--數學.files/image180.gif) ,則
,則--數學.files/image182.gif) ,又
,又--數學.files/image184.gif) .
.
∴--數學.files/image186.gif) 到
到--數學.files/image188.gif) 的距離等于
的距離等于--數學.files/image190.gif) . 即
. 即--數學.files/image192.gif) , ∴
, ∴--數學.files/image194.gif) .
.
∴直線--數學.files/image113.gif) 的方程為:
的方程為:--數學.files/image197.gif) 或
或--數學.files/image199.gif) .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com