
題目列表(包括答案和解析)
()某工廠有工人1000名, 其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人),現用分層抽樣方法(按A類、B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)。
(I)求甲、乙兩工人都被抽到的概率,其中甲為A類工人,乙為B類工人;
(II)從A類工人中的抽查結果和從B類工人中的抽插結果分別如下表1和表2.
表1:
| 生產能力分組 |
|
|
|
|
|
| 人數 | 4 | 8 |
| 5 | 3 |
表2:
| 生產能力分組 |
|
|
|
|
| 人數 | 6 | y | 36 | 18 |
(i)先確定x,y,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)
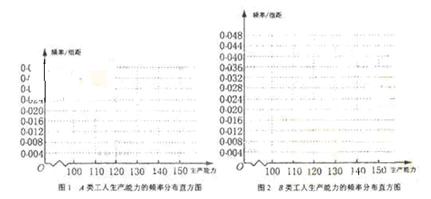
(ii)分別估計A類工人和B類工人生產能力的平均數,并估計該工廠工人的生產能力的平均數,同一組中的數據用該組區間的中點值作代表)
給出下列結論:
(1)在回歸分析中,可用相關指數R2的值判斷模型的擬合效果,R2越大,模型的擬合效果越好;
(2)某工產加工的某種鋼管,內徑與規定的內徑尺寸之差是離散型隨機變量;
(3)隨機變量的方差和標準差都反映了隨機變量的取值偏離于均值的平均程度,它們越小,則隨機變量偏離于均值的平均程度越小;
(4)若關于 的不等式
的不等式 在
在 上恒成立,則
上恒成立,則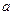 的最大值是1;
的最大值是1;
(5)甲、乙兩人向同一目標同時射擊一次,事件 :“甲、乙中至少一人擊中目標”與事件
:“甲、乙中至少一人擊中目標”與事件 :“甲,乙都沒有擊中目標”是相互獨立事件。
:“甲,乙都沒有擊中目標”是相互獨立事件。
其中結論正確的是 。(把所有正確結論的序號填上)
給出下列結論:
(1)在回歸分析中,可用相關指數R2的值判斷模型的擬合效果,R2越大,模型的擬合效果越好;
(2)某工產加工的某種鋼管,內徑與規定的內徑尺寸之差是離散型隨機變量;
(3)隨機變量的方差和標準差都反映了隨機變量的取值偏離于均值的平均程度,它們越小,則隨機變量偏離于均值的平均程度越小;
(4)若關于 的不等式
的不等式 在
在 上恒成立,則
上恒成立,則 的最大值是1;
的最大值是1;
(5)甲、乙兩人向同一目標同時射擊一次,事件 :“甲、乙中至少一人擊中目標”與事件
:“甲、乙中至少一人擊中目標”與事件 :“甲,乙都沒有擊中目標”是相互獨立事件。
:“甲,乙都沒有擊中目標”是相互獨立事件。
其中結論正確的是 。(把所有正確結論的序號填上)
已知點 (
( ),過點
),過點 作拋物線
作拋物線 的切線,切點分別為
的切線,切點分別為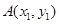 、
、 (其中
(其中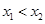 ).
).
(Ⅰ)若 ,求
,求 與
與 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,若以點 為圓心的圓
為圓心的圓 與直線
與直線 相切,求圓
相切,求圓 的方程;
的方程;
(Ⅲ)若直線 的方程是
的方程是 ,且以點
,且以點 為圓心的圓
為圓心的圓 與直線
與直線 相切,
相切,
求圓 面積的最小值.
面積的最小值.
【解析】本試題主要考查了拋物線的的方程以及性質的運用。直線與圓的位置關系的運用。
中∵直線 與曲線
與曲線 相切,且過點
相切,且過點 ,∴
,∴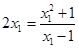 ,利用求根公式得到結論先求直線
,利用求根公式得到結論先求直線 的方程,再利用點P到直線的距離為半徑,從而得到圓的方程。
的方程,再利用點P到直線的距離為半徑,從而得到圓的方程。
(3)∵直線 的方程是
的方程是 ,
, ,且以點
,且以點 為圓心的圓
為圓心的圓 與直線
與直線 相切∴點
相切∴點 到直線
到直線 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即 ,借助于函數的性質圓
,借助于函數的性質圓 面積的最小值
面積的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直線 與曲線
與曲線 相切,且過點
相切,且過點 ,∴
,∴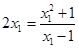 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵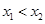 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,則
,則 的斜率
的斜率 ,
,
∴直線 的方程為:
的方程為: ,又
,又 ,
,
∴ ,即
,即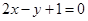 . -----------------7分
. -----------------7分
∵點 到直線
到直線 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即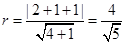 ,--------------8分
,--------------8分
故圓 的面積為
的面積為 . --------------------9分
. --------------------9分
(Ⅲ)∵直線 的方程是
的方程是 ,
, ,且以點
,且以點 為圓心的圓
為圓心的圓 與直線
與直線 相切∴點
相切∴點 到直線
到直線 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即 , ………10分
, ………10分
∴
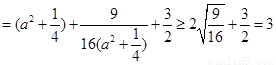 ,
,
當且僅當 ,即
,即 ,
, 時取等號.
時取等號.
故圓 面積的最小值
面積的最小值 .
.
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| a |
| b |
| b |
| c |
| b |
| 0 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com