
題目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
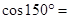 ( )
( )
A.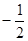 B.
B. C.
C.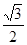 D.
D.
 =(
)
=(
)
A. B.
B. C.
C. D.
D.
一、選擇題: 本大題共12小題,每小題5分,共60分.
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
C
D
B
C
A
D
C
D
B
B
二、填空題:本大題共4小題,每小題4分,共16分.
13. 14.
14. 15.
15. 16.
16.
三、解答題:本大題共6小題,共74分.解答應寫出文字說明、證明過程或演算步驟.
17.(本小題滿分12分)
解:⑴f (x)= ?
? -1=(
-1=( sin2x,cosx)?(1,2cosx)-1
sin2x,cosx)?(1,2cosx)-1
= sin2x+2cos2x-1=
sin2x+2cos2x-1= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
3分
)
3分
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ 得kπ-
得kπ- ≤x≤kπ+
≤x≤kπ+
∴f (x)的遞增區間為 (k∈Z)
6分
(k∈Z)
6分
⑵f (A)=2sin( )=2 ∴sin(
)=2 ∴sin( )=1
)=1
∴ =
= ∴A=
∴A= 9分
9分
由正弦定理得:  .∴邊長b的值為
.∴邊長b的值為 .
12分
.
12分
18.(本小題滿分12分)
解: 將一顆骰子先后拋擲2次,此問題中含有36個等可能基本事件 1分
(1)記“兩數之和為
所以P(A)= ;
;
答:兩數之和為5的概率為 . 4分
. 4分
(2)記“兩數中至少有一個奇數”為事件B,則事件B與“兩數均為偶數”為對立事件,
所以P(B)= ;
;
答:兩數中至少有一個奇數的概率 .
8分
.
8分
(3)基本事件總數為36,點(x,y)在圓x2+y2=15的內部記為事件C,則C包含8個事件,
所以P(C)= .
.
答:點(x,y)在圓x2+y2=15的內部的概率 .
12分
.
12分
19.(本小題滿分12分)
 (1)證法1:如圖,取
(1)證法1:如圖,取 的中點
的中點 ,連接
,連接 ,
,
∵ 分別為
分別為 的中點,∴
的中點,∴ .
.
∵ 分別為
分別為 的中點,∴
的中點,∴ .
.
∴
 .
.
∴ 四點共面.………………………………………………………………2分
四點共面.………………………………………………………………2分
∵ 分別為
分別為 的中點,∴
的中點,∴ .……………………………………4分
.……………………………………4分
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .……………………………………………………………………6分
.……………………………………………………………………6分
證法2:∵ 分別為
分別為 的中點,
的中點,
∴ ,
, .……………………………………………………………2分
.……………………………………………………………2分
∵ ,∴
,∴ .又
.又
 …………………4分
…………………4分
∵ ,∴平面
,∴平面 平面
平面 . …………………5分
. …………………5分
∵ 平面
平面 ,∴
,∴ 平面
平面 . …………………………………………6分
. …………………………………………6分
(2)解:∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ .
.
∵ 為正方形,∴
為正方形,∴ .
.
∵ ,∴
,∴ 平面
平面 .……………………………………………8分
.……………………………………………8分
∵ ,
, ,∴
,∴ .……………10分
.……………10分
∵ ,
,
∴ .…………………………………12分
.…………………………………12分
20.(本小題滿分12分)
解:(1)∵
 …………………2分
…………………2分
(2)證明:

 是以
是以
 為首項,2為公比的等比數列. ………………7分
為首項,2為公比的等比數列. ………………7分
(3)由(I)得

 ………………12分
………………12分
21.(本小題滿分12分)
解:(1)設切線的斜率為k,則 ………2分
………2分
又 ,所以所求切線的方程為:
,所以所求切線的方程為: …………4分
…………4分
即 …………6分
…………6分
(2) , ∵
, ∵ 為單調增函數,∴
為單調增函數,∴
即對任意的 …………8分
…………8分

 …………10分
…………10分
而 ,當且僅當
,當且僅當 時,等號成立.
時,等號成立.
所以 …………12分
…………12分
22.(本小題滿分14分)
解:(1)由題意設橢圓的標準方程為 ,
,
由已知得: …………3分
…………3分
 橢圓的標準方程為
橢圓的標準方程為 .
…………5分
.
…………5分
(2)設 .
.
聯立 得:
得: , …………6分
, …………6分
則  …………8分
…………8分
又 .
.
因為以 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點 ,
,
 ,即
,即 .
…………9分
.
…………9分
 .
.
 .
.
 .
…………10分
.
…………10分
解得: ,且均滿足
,且均滿足 .
…………11分
.
…………11分
當 時,
時, 的方程
的方程 ,直線過點
,直線過點 ,與已知矛盾;…………12分
,與已知矛盾;…………12分
當 時,
時, 的方程為
的方程為 ,直線過定點
,直線過定點 . …………13分
. …………13分
所以,直線 過定點,定點坐標為
過定點,定點坐標為 .
…………14分
.
…………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com