
題目列表(包括答案和解析)
已知直線a、b、c和平面a、β,下列命題:①若a∥b,a∥a則a∥b;②若a^b,a^a,b^b,則a^b;③若a^b,a^b,則a∥a;④若a∥a,a^b,則a^b.其中正確的是( )
A.② B.①② C.①③ D.④
已知直三棱柱 中,
中,  ,
, ,
,
 是
是 和
和 的交點, 若
的交點, 若 .
.
(1)求 的長; (2)求點
的長; (2)求點 到平面
到平面 的距離;
的距離;
(3)求二面角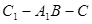 的平面角的正弦值的大小.
的平面角的正弦值的大小.

【解析】本試題主要考查了距離和角的求解運用。第一問中,利用ACC A
A 為正方形,
為正方形,  AC=3
AC=3
第二問中,利用面BB C
C C內(nèi)作CD
C內(nèi)作CD BC
BC ,
則CD就是點C平面A
,
則CD就是點C平面A BC
BC 的距離CD=
的距離CD= ,第三問中,利用三垂線定理作二面角的平面角,然后利用直角三角形求解得到其正弦值為
,第三問中,利用三垂線定理作二面角的平面角,然后利用直角三角形求解得到其正弦值為
解法一: (1)連AC 交A
交A C于E, 易證ACC
C于E, 易證ACC A
A 為正方形,
為正方形,  AC=3
…………… 5分
AC=3
…………… 5分
(2)在面BB C
C C內(nèi)作CD
C內(nèi)作CD BC
BC ,
則CD就是點C平面A
,
則CD就是點C平面A BC
BC 的距離CD=
的距離CD= … 8分
… 8分
(3) 易得AC
 面A
面A CB,
過E作EH
CB,
過E作EH A
A B于H, 連HC
B于H, 連HC ,
則HC
,
則HC
 A
A B
B

 C
C HE為二面角C
HE為二面角C -A
-A B-C的平面角. ……… 9分
B-C的平面角. ……… 9分
 sin
sin C
C HE=
HE=
 二面角C
二面角C -A
-A B-C的平面角的正弦大小為
B-C的平面角的正弦大小為 ……… 12分
……… 12分
解法二: (1)分別以直線C B、CC
B、CC 、C
、C A為x、y為軸建立空間直角坐標系, 設(shè)|CA|=h, 則C
A為x、y為軸建立空間直角坐標系, 設(shè)|CA|=h, 則C (0,
0, 0), B
(0,
0, 0), B (4,
0, 0), B(4, -3, 0), C(0, -3,
0), A
(4,
0, 0), B(4, -3, 0), C(0, -3,
0), A (0,
0, h), A(0, -3, h), G(2, -
(0,
0, h), A(0, -3, h), G(2, - , -
, - ) ……………………… 3分
) ……………………… 3分

 =(2, -
=(2, - , -
, - ),
),  =(0,
-3, -h(huán)) ……… 4分
=(0,
-3, -h(huán)) ……… 4分

 ·
· =0,
=0,
 h=3
h=3
(2)設(shè)平面A BC
BC 得法向量
得法向量 =(a, b, c),則可求得
=(a, b, c),則可求得 =(3, 4, 0) (令a=3)
=(3, 4, 0) (令a=3)
 點A到平面A
點A到平面A BC
BC 的距離為H=|
的距離為H=| |=
|= ……… 8分
……… 8分
(3) 設(shè)平面A BC的法向量為
BC的法向量為 =(x, y, z),則可求得
=(x, y, z),則可求得 =(0, 1, 1) (令z=1)
=(0, 1, 1) (令z=1)
 二面角C
二面角C -A
-A B-C的大小
B-C的大小 滿足cos
滿足cos =
= =
= ………
11分
………
11分
 二面角C
二面角C -A
-A B-C的平面角的正弦大小為
B-C的平面角的正弦大小為
一、選擇題:
1.B 2.C 3.B 4.A 5.A 6.B 7.D 8.D 9.C 10.D 11.C 12.B
二、填空題:
13.{2,3,4} 14.年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image142.gif) 15.
15.年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image144.gif) 16.①②④
16.①②④
三.17解:解: 年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image004.gif)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image009.gif) 所在的直線的斜率為
所在的直線的斜率為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image146.gif) =
=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image148.gif) ,………………(2分)
,………………(2分)
設(shè)直線年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image118.gif) 的斜率為
的斜率為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image150.gif) …………………………………………………(4分)
…………………………………………………(4分)
∴直線年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image118.gif) 的方程為:
的方程為:年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image152.gif) , …………………………………………………(6分)
, …………………………………………………(6分)
即年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image154.gif) ………………………………………………………………………(8分)
………………………………………………………………………(8分)
直線年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image118.gif) 與坐標軸的交點坐標為
與坐標軸的交點坐標為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image156.gif) …………………………………………(10分)
…………………………………………(10分)
∴直線年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image118.gif) 與坐標軸圍成的三角形的面積
與坐標軸圍成的三角形的面積年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image158.gif) ……………………(12分)
……………………(12分)
18.解:(1)∵AE∶EB=AH∶HD,∴EH//BD,CF∶FB=CG∶GD,
∴FG//BD,∴EH//FG, …………………………………………………(2分)
∵年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image160.gif) ,∴
,∴年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image162.gif) ,
,
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image163.gif) 同理
同理年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image165.gif) ,∴EH=FG
,∴EH=FG
∴EH年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image167.gif) FG
FG
故四邊形EFGH為平行四邊形. …………………(6分)
(2) ∵AE∶EB= CF∶FB,∴EF//AC,
又∵AC⊥BD,∴∠FEH是AC與BD所成的角,………………………(10分)
∴∠FEH=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image169.gif) ,從而EFGH為矩形,∴EG=FH. ………………………………(12分)
,從而EFGH為矩形,∴EG=FH. ………………………………(12分)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image171.gif) 19.解:解:(1)直觀圖如圖:
19.解:解:(1)直觀圖如圖:
…………………………………………………(6分)
(2)三棱錐底面是斜邊為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image173.gif) 的直角三角形.
的直角三角形.
其體積為V=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image175.gif) ………………………………(12分)
………………………………(12分)
20.解: (1)設(shè)每輛車的月租金定為x元,則租賃公司的月收益為:
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image017.gif) =(100-
=(100-年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image177.gif) )(x-150)-
)(x-150)-年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image177.gif) ×50,…………………(4分)
×50,…………………(4分)
整理得:年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image017.gif) =-
=-年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image179.gif) +162x-21000 …………………………………………………(6分)
+162x-21000 …………………………………………………(6分)
(2)每輛車的月租金為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image181.gif) 元…………………………………(8分)
元…………………………………(8分)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image183.gif) 時,
時,年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image017.gif)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image185.gif) 元
元
當租出了88輛車時,租賃公司的月收益303000元. ………………………………(12分)
21.解:年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image004.gif) 點的坐標為∠
點的坐標為∠年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image004.gif) 的平分線與
的平分線與年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image133.gif) 邊上的高所在直線的交點的坐標,即
邊上的高所在直線的交點的坐標,即
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image187.gif) ,解得
,解得年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image189.gif) ,
,年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image004.gif) 點的坐標為
點的坐標為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image191.gif) …………………………(4分)
…………………………(4分)
直線年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image133.gif) 的方程為
的方程為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image193.gif) ,即:
,即:年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image195.gif) ………………………(6分)
………………………(6分)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image009.gif) 點關(guān)于
點關(guān)于年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image137.gif) 的對稱點的坐標為
的對稱點的坐標為年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image197.gif) ,則
,則
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image199.gif) ,解得
,解得年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image201.gif) ,即
,即年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image203.gif) ………………………………………(8分)
………………………………………(8分)
直線年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image205.gif) 的方程為:
的方程為:年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image207.gif) ……………………………………………………(10分)
……………………………………………………(10分)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image011.gif) 的坐標是
的坐標是年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image133.gif) 與
與年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image205.gif) 交點的坐標:
交點的坐標:
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image209.gif) ,解得
,解得年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image211.gif) ,所以
,所以年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image011.gif) 的坐標
的坐標年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image213.gif) …………………………(12分)
…………………………(12分)
22.解:(1)∵ AB⊥平面BCD 年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image215.gif) 平面ABC⊥平面BCD
平面ABC⊥平面BCD 年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image215.gif) CD⊥平面ABC
CD⊥平面ABC
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image216.gif) AB
AB 年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image056.gif) 平面ABC ∠BCD=900
平面ABC ∠BCD=900
又∵年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image219.gif)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image215.gif) EF∥CD ……………………………(4分)
EF∥CD ……………………………(4分)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image215.gif) EF⊥平面ABC, ∴平面BEF⊥平面ABC………………(6分)
EF⊥平面ABC, ∴平面BEF⊥平面ABC………………(6分)
年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image220.gif) (2)平面BEF⊥平面ACD
(2)平面BEF⊥平面ACD
AC⊥EF 年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image215.gif) AC⊥平面BEF, ∴AC⊥BE………(8分)
AC⊥平面BEF, ∴AC⊥BE………(8分)
平面BEF∩平面ACD=EF
在Rt△BCD中,BD=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image222.gif) ,
,
在Rt△ABD中,AB=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image222.gif) ?tan60°=
?tan60°=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image080.gif) ……………………………………(10分)
……………………………………(10分)
在Rt△ABC中,AC=年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image226.gif) , ∴
, ∴年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image228.gif) ………………(12分)
………………(12分)
∴年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image230.gif) ,
,
即年高一上學(xué)期期末考試數(shù)學(xué)試題.files/image232.gif) 時,平面DEF⊥平面ACD. ……………………………………(14分)
時,平面DEF⊥平面ACD. ……………………………………(14分)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com