
題目列表(包括答案和解析)
設直線 與平面
與平面 相交但不垂直,則下列說法中正確的是
相交但不垂直,則下列說法中正確的是
A.在平面 內有且只有一條直線與直線
內有且只有一條直線與直線 平行
平行
B.過直線 有且只有一個平面與平面
有且只有一個平面與平面 平行
平行
C.與直線 平行的直線可能與平面
平行的直線可能與平面 垂直
垂直
D.與直線 垂直的平面不可能與平面
垂直的平面不可能與平面 平行
平行
設直線 與平面
與平面 相交但不垂直,則下列說法中正確的是
相交但不垂直,則下列說法中正確的是
A.在平面 內有且只有一條直線與直線
內有且只有一條直線與直線 垂直
垂直
B.過直線 有且只有一個平面與平面
有且只有一個平面與平面 垂直
垂直
C.與直線 垂直的直線不可能與平面
垂直的直線不可能與平面 平行
平行
D. 與直線 平行的平面不可能與平面
平行的平面不可能與平面 垂直
垂直
設直線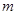 與平面
與平面 相交但不垂直,則下列說法中正確的是 ( )
相交但不垂直,則下列說法中正確的是 ( )
A.在平面 內有且只有一條直線與直線
內有且只有一條直線與直線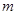 垂直
垂直
B.過直線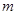 有且只有一個平面與平面
有且只有一個平面與平面 垂直
垂直
C.過直線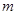 垂直的直線不可能與平面
垂直的直線不可能與平面 平行
平行
D.與直線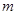 平行的平面不可能與平面
平行的平面不可能與平面 垂直
垂直
設直線 與平面
與平面 相交但不垂直,則下列說法中正確的是
相交但不垂直,則下列說法中正確的是
A.在平面 內有且只有一條直線與直線
內有且只有一條直線與直線 垂直
垂直
B.過直線 有且只有一個平面與平面
有且只有一個平面與平面 垂直
垂直
C.與直線 垂直的直線不可能與平面
垂直的直線不可能與平面 平行
平行
D.與直線 平行的平面不可能與平面
平行的平面不可能與平面 垂直
垂直
A.在平面![]() 內有且只有一條直線與直線
內有且只有一條直線與直線![]() 垂直
垂直
B.過直線![]() 有且只有一個平面與平面
有且只有一個平面與平面![]() 垂直
垂直
C.與直線![]() 垂直的直線不可能與平面
垂直的直線不可能與平面![]() 平行
平行
D.與直線![]() 平行的平面不可能與平面
平行的平面不可能與平面![]() 垂直
垂直
一、選擇題:本大題共12小題,每小題5分,共60分。
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
C
A
A
C
D
B
D
C
C
1.B.因含詳解.files/image024.gif)
含詳解.files/image291.gif)
含詳解.files/image026.gif) 但
但含詳解.files/image026.gif)
含詳解.files/image293.gif)
含詳解.files/image024.gif) 。
。
2.含詳解.files/image295.gif) .因
.因含詳解.files/image297.gif) ,
,
3.B. 因為含詳解.files/image147.gif) 的定義域為[0,2],所以對
的定義域為[0,2],所以對含詳解.files/image149.gif) ,
,含詳解.files/image301.gif) 但
但含詳解.files/image303.gif) 故
故含詳解.files/image305.gif) 。
。
4.含詳解.files/image278.gif) 函數
函數含詳解.files/image308.gif) 為增函數
為增函數
5.含詳解.files/image012.gif)
含詳解.files/image311.gif) ,
,含詳解.files/image313.gif) ,…,
,…,含詳解.files/image315.gif)
含詳解.files/image317.gif)
6.含詳解.files/image319.gif)
含詳解.files/image321.gif)
含詳解.files/image323.gif)
7. 含詳解.files/image278.gif) .由題知,垂足的軌跡為以焦距為直徑的圓,則
.由題知,垂足的軌跡為以焦距為直徑的圓,則含詳解.files/image325.gif)
又含詳解.files/image327.gif) ,所以
,所以含詳解.files/image329.gif)
8. 含詳解.files/image295.gif)
含詳解.files/image331.gif)
9. 含詳解.files/image278.gif) .
.
10.含詳解.files/image295.gif) ..函數
..函數含詳解.files/image333.gif)
11.含詳解.files/image278.gif) .一天顯示的時間總共有
.一天顯示的時間總共有含詳解.files/image335.gif) 種,和為23總共有4種,故所求概率為
種,和為23總共有4種,故所求概率為含詳解.files/image137.gif) .
.
12.含詳解.files/image278.gif) .當
.當含詳解.files/image338.gif) 時,顯然成立
時,顯然成立
當含詳解.files/image340.gif) 時,顯然不成立;當
時,顯然不成立;當含詳解.files/image342.gif) 顯然成立;
顯然成立;
當含詳解.files/image344.gif) 時
時含詳解.files/image346.gif) ,則
,則含詳解.files/image348.gif) 兩根為負,結論成立
兩根為負,結論成立
故含詳解.files/image350.gif)
二、填空題:本大題共4小題,每小題4分,共16分。
13.
含詳解.files/image352.gif) 14..
14.. 含詳解.files/image354.gif)
含詳解.files/image356.gif) 15.
5
16. A、B、D
15.
5
16. A、B、D
13.依題意含詳解.files/image358.gif)
含詳解.files/image360.gif)
14. 含詳解.files/image356.gif)
15. 易求得含詳解.files/image088.gif) 、
、含詳解.files/image285.gif) 到球心
到球心含詳解.files/image364.gif) 的距離分別為3、2,類比平面內圓的情形可知當
的距離分別為3、2,類比平面內圓的情形可知當含詳解.files/image088.gif) 、
、含詳解.files/image285.gif) 與球心
與球心含詳解.files/image364.gif) 共線時,
共線時,含詳解.files/image366.gif) 取最大值5。
取最大值5。
16.含詳解.files/image368.gif) , ∴
, ∴含詳解.files/image012.gif) 對
對
取含詳解.files/image371.gif) 的中點
的中點含詳解.files/image364.gif) ,則
,則含詳解.files/image374.gif) , ∴
, ∴含詳解.files/image274.gif) 對
對
設含詳解.files/image377.gif) , 則
, 則含詳解.files/image379.gif) ,而
,而含詳解.files/image381.gif) ,∴
,∴含詳解.files/image278.gif) 錯
錯
又含詳解.files/image384.gif) ,∴
,∴含詳解.files/image295.gif) 對
對
∴真命題的代號是含詳解.files/image387.gif)
三、解答題:本大題共6小題,共74分。
17.解:(1)由含詳解.files/image192.gif)
含詳解.files/image389.gif)
得含詳解.files/image391.gif) ,
,含詳解.files/image393.gif)
于是含詳解.files/image196.gif) =
=含詳解.files/image395.gif) .
.
(2)因為含詳解.files/image397.gif)
所以含詳解.files/image399.gif)
含詳解.files/image401.gif)
含詳解.files/image403.gif)
含詳解.files/image147.gif) 的最大值為
的最大值為含詳解.files/image406.gif) .
.
18.解:(1)令A表示兩年后柑桔產量恰好達到災前產量這一事件
含詳解.files/image408.gif)
(2)令B表示兩年后柑桔產量超過災前產量這一事件
含詳解.files/image410.gif)
19.(1)設含詳解.files/image060.gif) 的公差為
的公差為含詳解.files/image412.gif) ,
,含詳解.files/image206.gif) 的公比為
的公比為含詳解.files/image414.gif) ,則
,則含詳解.files/image412.gif) 為正整數,
為正整數,
含詳解.files/image416.gif) ,
,含詳解.files/image418.gif)
依題意有含詳解.files/image420.gif) ①
①
解得含詳解.files/image422.gif) 或
或含詳解.files/image424.gif) (舍去)
(舍去)
故含詳解.files/image426.gif)
(2)含詳解.files/image428.gif)
∴含詳解.files/image430.gif)
含詳解.files/image432.gif)
含詳解.files/image434.gif)
含詳解.files/image436.gif)
20.解 :(1)證明:依題設,含詳解.files/image240.gif) 是
是含詳解.files/image438.gif) 的中位線,所以
的中位線,所以含詳解.files/image240.gif) ∥
∥含詳解.files/image440.gif) ,
,
含詳解.files/image442.gif) 則
則含詳解.files/image240.gif) ∥平面
∥平面含詳解.files/image444.gif) ,所以
,所以含詳解.files/image240.gif) ∥
∥含詳解.files/image250.gif) 。
。
又含詳解.files/image238.gif) 是
是含詳解.files/image240.gif) 的中點,所以
的中點,所以含詳解.files/image446.gif) ⊥
⊥含詳解.files/image240.gif) ,
,
則含詳解.files/image446.gif) ⊥
⊥含詳解.files/image250.gif) 。
。
因為含詳解.files/image224.gif) ⊥
⊥含詳解.files/image226.gif) ,
,含詳解.files/image224.gif) ⊥
⊥含詳解.files/image228.gif) ,
,
所以含詳解.files/image224.gif) ⊥面
⊥面含詳解.files/image444.gif) ,則
,則含詳解.files/image224.gif) ⊥
⊥含詳解.files/image250.gif) ,
,
因此含詳解.files/image250.gif) ⊥面
⊥面含詳解.files/image252.gif) 。
。
(2)作含詳解.files/image448.gif) ⊥
⊥含詳解.files/image450.gif) 于
于含詳解.files/image285.gif) ,連
,連含詳解.files/image453.gif) 。
。
因為含詳解.files/image455.gif) ⊥平面
⊥平面含詳解.files/image457.gif) ,
,
根據三垂線定理知,含詳解.files/image453.gif) ⊥
⊥含詳解.files/image450.gif) ,
,
含詳解.files/image460.gif) 就是二面角
就是二面角含詳解.files/image254.gif) 的平面角。
的平面角。
作含詳解.files/image462.gif) ⊥
⊥含詳解.files/image464.gif) 于
于含詳解.files/image088.gif) ,則
,則含詳解.files/image462.gif) ∥
∥含詳解.files/image224.gif) ,則
,則含詳解.files/image088.gif) 是
是含詳解.files/image226.gif) 的中點,則
的中點,則含詳解.files/image470.gif) 。
。
設含詳解.files/image472.gif) ,由
,由含詳解.files/image474.gif) 得,
得,含詳解.files/image476.gif) ,解得
,解得含詳解.files/image478.gif) ,
,
在含詳解.files/image480.gif) 中,
中,含詳解.files/image482.gif) ,則,
,則,含詳解.files/image484.gif) 。
。
所以含詳解.files/image486.gif) ,故二面角
,故二面角含詳解.files/image254.gif) 為
為含詳解.files/image488.gif) 。
。
解法二:(1)以直線含詳解.files/image490.gif) 分別為
分別為含詳解.files/image492.gif) 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,含詳解.files/image494.gif) 則
則
含詳解.files/image496.gif)
所以含詳解.files/image498.gif)
所以含詳解.files/image500.gif)
所以含詳解.files/image502.gif) 平面
平面含詳解.files/image252.gif)
由含詳解.files/image240.gif) ∥
∥含詳解.files/image440.gif) 得
得含詳解.files/image250.gif) ∥
∥含詳解.files/image440.gif) ,故:
,故:含詳解.files/image508.gif) 平面
平面含詳解.files/image252.gif)
(2)由已知含詳解.files/image510.gif) 設
設含詳解.files/image512.gif)
含詳解.files/image517.gif) 則
則含詳解.files/image519.gif)
由含詳解.files/image521.gif) 與
與含詳解.files/image523.gif) 共線得:存在
共線得:存在含詳解.files/image525.gif) 有
有含詳解.files/image527.gif) 得
得
含詳解.files/image529.gif)
同理:含詳解.files/image531.gif)
含詳解.files/image533.gif)
設含詳解.files/image535.gif) 是平面
是平面含詳解.files/image537.gif) 的一個法向量,
的一個法向量,
則含詳解.files/image539.gif) 令
令含詳解.files/image541.gif) 得
得含詳解.files/image543.gif)
含詳解.files/image545.gif)
又含詳解.files/image547.gif) 是平面
是平面含詳解.files/image457.gif) 的一個法量
的一個法量
含詳解.files/image550.gif)
所以二面角的大小為含詳解.files/image552.gif)
21. 解:(1)因為含詳解.files/image554.gif)
令含詳解.files/image556.gif) 得
得含詳解.files/image558.gif)
由含詳解.files/image560.gif) 時,
時,含詳解.files/image562.gif) 在
在含詳解.files/image556.gif) 根的左右的符號如下表所示
根的左右的符號如下表所示
含詳解.files/image145.gif)
含詳解.files/image566.gif)
含詳解.files/image568.gif)
含詳解.files/image570.gif)
含詳解.files/image572.gif)
含詳解.files/image574.gif)
含詳解.files/image262.gif)
含詳解.files/image577.gif)
含詳解.files/image562.gif)
含詳解.files/image580.gif)
含詳解.files/image572.gif)
含詳解.files/image583.gif)
含詳解.files/image572.gif)
含詳解.files/image580.gif)
含詳解.files/image572.gif)
含詳解.files/image583.gif)
含詳解.files/image147.gif)
含詳解.files/image586.gif)
極小值
含詳解.files/image588.gif)
極大值
含詳解.files/image586.gif)
極小值
含詳解.files/image588.gif)
所以含詳解.files/image147.gif) 的遞增區間為
的遞增區間為含詳解.files/image591.gif)
含詳解.files/image147.gif) 的遞減區間為
的遞減區間為含詳解.files/image593.gif)
(2)由(1)得到含詳解.files/image595.gif) ,
,含詳解.files/image597.gif)
含詳解.files/image599.gif)
要使含詳解.files/image147.gif) 的圖像與直線
的圖像與直線含詳解.files/image260.gif) 恰有兩個交點,只要
恰有兩個交點,只要含詳解.files/image602.gif) 或
或含詳解.files/image604.gif) ,
,
即含詳解.files/image606.gif) 或
或含詳解.files/image608.gif) .
.
22.(1)證明:設含詳解.files/image610.gif) ,
,含詳解.files/image612.gif)
則直線含詳解.files/image234.gif) 的方程:
的方程:含詳解.files/image615.gif)
即:含詳解.files/image617.gif)
因含詳解.files/image619.gif) 在
在含詳解.files/image234.gif) 上,所以
上,所以含詳解.files/image621.gif) ①
①
又直線含詳解.files/image623.gif) 方程:
方程:含詳解.files/image625.gif)
由含詳解.files/image627.gif) 得:
得:含詳解.files/image629.gif)
所以含詳解.files/image631.gif)
同理,含詳解.files/image633.gif)
所以直線含詳解.files/image240.gif) 的方程:
的方程:含詳解.files/image636.gif)
令含詳解.files/image638.gif) 得
得含詳解.files/image640.gif)
將①代入上式得含詳解.files/image642.gif) ,即
,即含詳解.files/image285.gif) 點在直線
點在直線含詳解.files/image240.gif) 上
上
所以含詳解.files/image646.gif) 三點共線
三點共線
(2)解:由已知含詳解.files/image648.gif) 共線,所以
共線,所以含詳解.files/image650.gif)
以含詳解.files/image234.gif) 為直徑的圓的方程:
為直徑的圓的方程:含詳解.files/image653.gif)
由含詳解.files/image655.gif) 得
得含詳解.files/image657.gif)
所以含詳解.files/image642.gif) (舍去),
(舍去),含詳解.files/image660.gif)
要使圓與拋物線有異于含詳解.files/image662.gif) 的交點,則
的交點,則含詳解.files/image664.gif)
所以存在含詳解.files/image666.gif) ,使以
,使以含詳解.files/image234.gif) 為直徑的圓與拋物線有異于
為直徑的圓與拋物線有異于含詳解.files/image662.gif) 的交點
的交點含詳解.files/image669.gif)
則含詳解.files/image671.gif)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com