精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

在給定的直角坐標系中，根據坐標描出點的位置、由點的位置寫出它的坐標；
在平面直角坐標系中，點在第三象限，則m的取值范圍是

A．

B．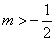

C．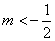

D．

通過學習三角函數，我們知道在直角三角形中，一個銳角的大小與兩條邊長的比值相互唯一確定，因此邊長與角的大小之間可以相互轉化．類似的，可以在等腰三角形中建立邊角之間的聯系．我們定義：等腰三角形中底邊與腰的比叫做頂角正對（sad），如圖①，在△ABC中，AB=AC，頂角A的正對記作sadA，這時sadA=底邊/腰=．容易知道一個角的大小與這個角的正對值也是相互唯一確定的．根據上述角的正對定義，解下列問題：
（1）sad60°=　    　．
（2）對于0°＜A＜180°，∠A的正對值sadA的取值范圍是　       　．
（3）如圖②，已知sinA=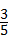，其中∠A為銳角，試求sadA的值．

若點P（a，b）在第四象限內，則a，b的取值范圍是（    ）

如圖1，已知等邊△ABC的邊長為1，D、E、F分別是AB、BC、AC邊上的點（均不與點A、B、C重合），記△DEF的周長為.

（1）若D、E、F分別是AB、BC、AC邊上的中點，則=_______；
（2）若D、E、F分別是AB、BC、AC邊上任意點，則的取值范圍是            .
小亮和小明對第（2）問中的最小值進行了討論，小亮先提出了自己的想法：將以AC邊為軸翻折一次得，再將以為軸翻折一次得，如圖2所示. 則由軸對稱的性質可知，，根據兩點之間線段最短，可得. 老師聽了后說：“你的想法很好，但的長度會因點D的位置變化而變化，所以還得不出我們想要的結果.”小明接過老師的話說：“那我們繼續再翻折3次就可以了”.請參考他們的想法，寫出你的答案.

已知拋物線y＝ax²＋bx＋c的部分圖象如圖所示，若y＞0，則x的取值范圍是_____________．