
題目列表(包括答案和解析)
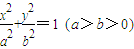 的離心率是
的離心率是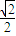 ,P1、P2是橢圓E的長(zhǎng)軸的兩個(gè)端點(diǎn)(P2位于P1右側(cè)),點(diǎn)F是橢圓E的右焦點(diǎn).點(diǎn)Q是x軸上位于P2右側(cè)的一點(diǎn),且滿足
,P1、P2是橢圓E的長(zhǎng)軸的兩個(gè)端點(diǎn)(P2位于P1右側(cè)),點(diǎn)F是橢圓E的右焦點(diǎn).點(diǎn)Q是x軸上位于P2右側(cè)的一點(diǎn),且滿足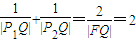 .
.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 2 |
已知曲線 上動(dòng)點(diǎn)
上動(dòng)點(diǎn) 到定點(diǎn)
到定點(diǎn) 與定直線
與定直線 的距離之比為常數(shù)
的距離之比為常數(shù) .
.
(1)求曲線 的軌跡方程;
的軌跡方程;
(2)若過(guò)點(diǎn) 引曲線C的弦AB恰好被點(diǎn)
引曲線C的弦AB恰好被點(diǎn) 平分,求弦AB所在的直線方程;
平分,求弦AB所在的直線方程;
(3)以曲線 的左頂點(diǎn)
的左頂點(diǎn) 為圓心作圓
為圓心作圓 :
: ,設(shè)圓
,設(shè)圓 與曲線
與曲線 交于點(diǎn)
交于點(diǎn) 與點(diǎn)
與點(diǎn) ,求
,求 的最小值,并求此時(shí)圓
的最小值,并求此時(shí)圓 的方程.
的方程.
【解析】第一問(wèn)利用(1)過(guò)點(diǎn) 作直線
作直線 的垂線,垂足為D.
的垂線,垂足為D.
 代入坐標(biāo)得到
代入坐標(biāo)得到
第二問(wèn)當(dāng)斜率k不存在時(shí),檢驗(yàn)得不符合要求;
當(dāng)直線l的斜率為k時(shí), ;,化簡(jiǎn)得
;,化簡(jiǎn)得

第三問(wèn)點(diǎn)N與點(diǎn)M關(guān)于X軸對(duì)稱,設(shè) ,, 不妨設(shè)
,, 不妨設(shè) .
.
由于點(diǎn)M在橢圓C上,所以 .
.
由已知 ,則
,則
 ,
,
由于 ,故當(dāng)
,故當(dāng) 時(shí),
時(shí), 取得最小值為
取得最小值為 .
.
計(jì)算得, ,故
,故 ,又點(diǎn)
,又點(diǎn) 在圓
在圓 上,代入圓的方程得到
上,代入圓的方程得到 .
.
故圓T的方程為:
(本小題滿分12分)
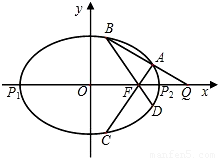
如圖,點(diǎn)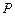 是橢圓
是橢圓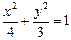 上一動(dòng)點(diǎn),點(diǎn)
上一動(dòng)點(diǎn),點(diǎn) 是點(diǎn)
是點(diǎn) 在
在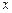 軸上的射影,坐標(biāo)平面
軸上的射影,坐標(biāo)平面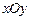 內(nèi)動(dòng)點(diǎn)
內(nèi)動(dòng)點(diǎn) 滿足:
滿足: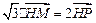 (
( 為坐標(biāo)原點(diǎn)),設(shè)動(dòng)點(diǎn)
為坐標(biāo)原點(diǎn)),設(shè)動(dòng)點(diǎn) 的軌跡為曲線
的軌跡為曲線 .
.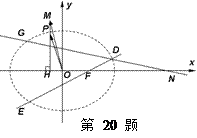
(Ⅰ)求曲線 的方程并畫出草圖;
的方程并畫出草圖;
(Ⅱ)過(guò)右焦點(diǎn)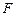 的直線
的直線 交曲線
交曲線 于
于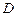 ,
,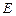 兩點(diǎn),且
兩點(diǎn),且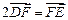 ,點(diǎn)
,點(diǎn)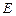 關(guān)于
關(guān)于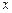 軸的對(duì)稱點(diǎn)為
軸的對(duì)稱點(diǎn)為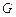 ,求直線
,求直線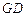 的方程.
的方程.
(本小題滿分12分)
如圖,點(diǎn)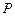 是橢圓
是橢圓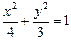 上一動(dòng)點(diǎn),點(diǎn)
上一動(dòng)點(diǎn),點(diǎn) 是點(diǎn)
是點(diǎn)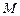 在
在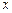 軸上的射影,坐標(biāo)平面
軸上的射影,坐標(biāo)平面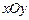 內(nèi)動(dòng)點(diǎn)
內(nèi)動(dòng)點(diǎn)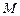 滿足:
滿足: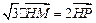 (
( 為坐標(biāo)原點(diǎn)),設(shè)動(dòng)點(diǎn)
為坐標(biāo)原點(diǎn)),設(shè)動(dòng)點(diǎn)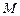 的軌跡為曲線
的軌跡為曲線 .
.
(Ⅰ)求曲線 的方程并畫出草圖;
的方程并畫出草圖;
(Ⅱ)過(guò)右焦點(diǎn)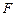 的直線
的直線 交曲線
交曲線 于
于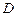 ,
,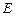 兩點(diǎn),且
兩點(diǎn),且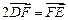 ,點(diǎn)
,點(diǎn)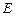 關(guān)于
關(guān)于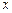 軸的對(duì)稱點(diǎn)為
軸的對(duì)稱點(diǎn)為 ,求直線
,求直線 的方程.
的方程.
一、選擇題
AACCD BBDDD AC
二、填空題
13.年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image248.gif) 14.T13 15.①⑤ 16.
14.T13 15.①⑤ 16.年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image250.gif)
三、解答題
17.解:(Ⅰ)因?yàn)?sub>年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image158.gif) ,
,
由正弦定理,得年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image252.gif) ,
……3分
,
……3分
整理,得年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image254.gif)
因?yàn)?sub>年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image146.gif) 、
、年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image148.gif) 、
、年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) 是
是年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image144.gif) 的三內(nèi)角,所以
的三內(nèi)角,所以年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image256.gif) ,
,
因此 年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image258.gif) .
……6分
.
……6分
(Ⅱ)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image260.gif) ,即
,即年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image262.gif) ,
……8分
,
……8分
由余弦定理,得年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image264.gif) ,所以
,所以年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image266.gif) , ……10分
, ……10分
解方程組年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image268.gif) ,得
,得年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image270.gif) .
……12分
.
……12分
18.(本題滿分12分)
解法一:記年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image272.gif) 與
與年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image274.gif) 的比賽為
的比賽為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image276.gif) ,
,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image278.gif)
(Ⅰ)齊王與田忌賽馬,有如下六種情況:
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image280.gif) ,
,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image282.gif) ,
,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image284.gif) ,
, 年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image286.gif) ,
,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image288.gif) ,
, 年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image290.gif) . ………………………3分
. ………………………3分
其中田忌獲勝的只有一種年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image286.gif) ,所以田忌獲勝的概率為
,所以田忌獲勝的概率為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image292.gif) .
.
…………………………………………………………………………………………6分
(Ⅱ)已知齊王第一場(chǎng)必出上等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image294.gif) ,若田忌第一場(chǎng)出上等馬
,若田忌第一場(chǎng)出上等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif) 或中等馬
或中等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif) ,則剩下兩場(chǎng)中至少輸?shù)粢粓?chǎng),這時(shí)田忌必?cái)。?/p>
,則剩下兩場(chǎng)中至少輸?shù)粢粓?chǎng),這時(shí)田忌必?cái)。?/p>
為了使自己獲勝的概率最大,田忌第一場(chǎng)應(yīng)出下等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif) ,后兩場(chǎng)有兩種情形:
,后兩場(chǎng)有兩種情形:
①若齊王第二場(chǎng)派出中等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image302.gif) ,可能對(duì)陣情形是
,可能對(duì)陣情形是年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image304.gif) 、
、年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image306.gif)
或者年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image308.gif) 、
、年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image310.gif) ,所以田忌獲勝的概率為
,所以田忌獲勝的概率為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image312.gif) ; ………………………9分
; ………………………9分
②若齊王第二場(chǎng)派出下等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image314.gif) ,可能對(duì)陣情形是
,可能對(duì)陣情形是年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image310.gif) 、
、年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image308.gif)
或者年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image306.gif) 、
、年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image304.gif) ,所以田忌獲勝的概率為
,所以田忌獲勝的概率為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image312.gif) ,
,
所以田忌按年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image320.gif) 或者
或者年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image322.gif) 的順序出馬,才能使自己獲勝的概率達(dá)到最大值
的順序出馬,才能使自己獲勝的概率達(dá)到最大值年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image312.gif) .
.
………………………………………………………………………………………12分
解法二:各種對(duì)陣情況列成下列表格:
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image294.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image302.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image314.gif)
1
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif)
2
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif)
3
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif)
4
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif)
5
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif)
6
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image298.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image296.gif)
………………………3分
(Ⅰ)其中田忌獲勝的只有第五種這一種情形,所以田忌獲勝的概率為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image292.gif) .……6分
.……6分
(Ⅱ)為了使自己獲勝的概率最大,田忌第一場(chǎng)應(yīng)出下等馬年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image300.gif) ,即只能是第五、第六兩種情形. …………………………………………………9分
,即只能是第五、第六兩種情形. …………………………………………………9分
其中田忌獲勝的只有第五種這一種情形,所以田忌按年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image320.gif) 或者
或者年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image322.gif) 的順序出馬,才能使自己獲勝的概率達(dá)到最大值
的順序出馬,才能使自己獲勝的概率達(dá)到最大值年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image312.gif) .………………………12分
.………………………12分
19.(本題滿分12分)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image341.gif) 解證: (Ⅰ) 連結(jié)
解證: (Ⅰ) 連結(jié)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image343.gif) 連結(jié)
連結(jié)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image345.gif) ,
,
∵四邊形年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image180.gif) 是矩形
是矩形
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image135.gif) 為
為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image348.gif) 中點(diǎn)
中點(diǎn)
又年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image350.gif) 為
為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image187.gif) 中點(diǎn),從而
中點(diǎn),從而年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image345.gif) ∥
∥年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image191.gif) ------------3分
------------3分
∵年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image354.gif) 平面
平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image193.gif) ,
,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image356.gif) 平面
平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image193.gif)
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image191.gif) ∥平面
∥平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image193.gif) 。-----------------------5分
。-----------------------5分
(Ⅱ)(方法1)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image358.gif)
三角形年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image360.gif) 的面積
的面積年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image362.gif) -------------------8分
-------------------8分
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image146.gif) 到平面
到平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image180.gif) 的距離為
的距離為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image144.gif) 的高
的高年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image367.gif)
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image369.gif) ---------------------------------11分
---------------------------------11分
因此,三棱錐年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image195.gif) 的體積為
的體積為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image030.gif) 。------------------------------------12分
。------------------------------------12分
(方法2)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image358.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image371.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image373.gif) ,
,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image375.gif) ,
,
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image377.gif) 為等腰
為等腰年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image379.gif) ,取底邊
,取底邊年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image381.gif) 的中點(diǎn)
的中點(diǎn)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image383.gif) ,
,
則年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image385.gif) ,
,
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image377.gif) 的面積
的面積年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image387.gif) -----------8分
-----------8分
∵年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image389.gif) ,∴點(diǎn)
,∴點(diǎn)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image391.gif) 到平面
到平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image393.gif) 的距離等于
的距離等于年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) 到平面
到平面
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image393.gif) 的距離,
的距離,
由于年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image396.gif) ,
,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image398.gif) ,
,
∴ 年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image400.gif) ,
,
過(guò)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) 作
作年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image402.gif) 于
于年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image404.gif) ,則
,則年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image406.gif) 就是
就是年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) 到平面
到平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image393.gif) 的距離,
的距離,
又年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image408.gif) ,----------11分
,----------11分
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image410.gif) ---------------------12分
---------------------12分
(方法3)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image412.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image146.gif) 到平面
到平面年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image180.gif) 的距離為
的距離為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image144.gif) 的高
的高年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image367.gif)
∴四棱錐年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image172.gif) 的體積
的體積年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image415.gif) ------------------------9分
------------------------9分
三棱錐年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image417.gif) 的體積
的體積年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image419.gif)
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image421.gif) ---------------------------------------------11分
---------------------------------------------11分
因此,三棱錐年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image195.gif) 的體積為
的體積為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image030.gif) 。-------------------------------------12分
。-------------------------------------12分
20.(Ⅰ)依題意知,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image423.gif)
∵年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image425.gif) ,
,
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image427.gif) .
.
∴所求橢圓年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) 的方程為
的方程為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image429.gif) .
……4分
.
……4分
(Ⅱ)設(shè)點(diǎn)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image137.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image211.gif) 關(guān)于直線
關(guān)于直線年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image213.gif) 的對(duì)稱點(diǎn)為
的對(duì)稱點(diǎn)為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image215.gif) ,
,
∴ 年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image432.gif) ……6分
……6分
解得:年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image434.gif) ,
,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image436.gif) .
……8分
.
……8分
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image438.gif) .
……10分
.
……10分
∵ 點(diǎn)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image137.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image211.gif) 在橢圓
在橢圓年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) :
:年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image429.gif) 上,
上,
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image440.gif) , 則
, 則年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image442.gif) .
.
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image217.gif) 的取值范圍為
的取值范圍為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image445.gif) .
……12分
.
……12分
21.解:(Ⅰ)由年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image219.gif) 知,
知,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image447.gif) 定義域?yàn)?sub>
定義域?yàn)?sub>年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image449.gif) ,
,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image451.gif) . ……………………3分
. ……………………3分
當(dāng)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image453.gif) 時(shí),
時(shí),年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image455.gif) ,
………………4分
,
………………4分
當(dāng)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image457.gif) 時(shí),
時(shí),年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image459.gif) .
………………5分
.
………………5分
所以年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image221.gif) 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image462.gif) ,
,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image221.gif) 的單調(diào)減區(qū)間是
的單調(diào)減區(qū)間是年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image464.gif) .
…………………… ………………6分
.
…………………… ………………6分
(Ⅱ)由(Ⅰ)知,年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image221.gif) 在
在年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image466.gif) 上單調(diào)遞增,
上單調(diào)遞增,
在年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image464.gif) 上單調(diào)遞減,在
上單調(diào)遞減,在年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image469.gif) 上單調(diào)遞增,且當(dāng)
上單調(diào)遞增,且當(dāng)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image471.gif) 或
或年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image473.gif) 時(shí),
時(shí),
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image475.gif) , 所以
, 所以年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image221.gif) 的極大值為
的極大值為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image477.gif) ,
,
極小值為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image479.gif) . ………………………8分
. ………………………8分
又因?yàn)?sub>年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image481.gif) ,
,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image483.gif) , ………10分
, ………10分
所以在年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image221.gif) 的三個(gè)單調(diào)區(qū)間
的三個(gè)單調(diào)區(qū)間年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image486.gif) 上,
上,
直線年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image223.gif) 與
與年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image489.gif) 的圖象各有一個(gè)交點(diǎn),
的圖象各有一個(gè)交點(diǎn),
當(dāng)且僅當(dāng)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image491.gif) , 因此,
, 因此,
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image154.gif) 的取值范圍為
的取值范圍為年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image493.gif) . ………………12分
. ………………12分
22.解:(Ⅰ)當(dāng)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image245.gif) 時(shí),
時(shí),年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image495.gif) ……………………………3分
……………………………3分
∴年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image243.gif) =
=年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image497.gif)
=年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image499.gif)
=年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image501.gif)
=年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image503.gif) …………………………………7分
…………………………………7分
(Ⅱ) 年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image505.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image507.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image509.gif) +
+年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image511.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image513.gif) +
+年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image515.gif)
年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image517.gif)
=年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image519.gif)
=年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image521.gif) ……………13分
……………13分
當(dāng)且僅當(dāng)年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image523.gif) ,即
,即年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image525.gif) 時(shí),
時(shí),年度高三5月檢測(cè)題----文科數(shù)學(xué).files/image150.gif) 最小.……………………14分
最小.……………………14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com