
【題目】已知橢圓![]() 經過點
經過點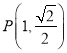 ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,不經過
的左、右焦點,不經過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩個不同的點
交于兩個不同的點![]() ,如果直線
,如果直線![]() 、
、![]() 、
、![]() 的斜率依次成等差數列,求焦點
的斜率依次成等差數列,求焦點![]() 到直線
到直線![]() 的距離
的距離![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】試題分析:(1)由已知條件算出![]() 的值,得出橢圓C的方程;(2)設
的值,得出橢圓C的方程;(2)設![]() ,
, ![]() ,直線
,直線![]() 的方程為
的方程為![]() ,代入橢圓方程中,消去
,代入橢圓方程中,消去![]() 得
得![]() ,由韋達定理求出
,由韋達定理求出![]() 的值,利用直線
的值,利用直線![]() 、
、![]() 、
、![]() 的斜率依次成等差數列,得到
的斜率依次成等差數列,得到![]() ,從而
,從而![]() ,即
,即![]() ,化簡得
,化簡得![]() ,由點到直線的距離,求出
,由點到直線的距離,求出![]() 的表達式,通過借助函數
的表達式,通過借助函數![]() 的單調性,求出
的單調性,求出![]() 的范圍。
的范圍。
試題解析(1)由題意,知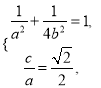 考慮到
考慮到![]() ,解得
,解得![]()
所以,所求橢圓C的方程為![]() .
.
(2)設直線![]() 的方程為
的方程為![]() ,代入橢圓方程
,代入橢圓方程![]() ,
,
整理得![]() .
.
由![]() ,得
,得![]() . ①
. ①
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
因為![]() ,所以
,所以![]() ,
, ![]() .
.
因為![]() ,且
,且![]() ,
, ![]() ,
,
所以![]() .
.
因為直線AB: ![]() 不過焦點
不過焦點![]() ,所以
,所以![]() ,
,
所以![]() ,從而
,從而![]() ,即
,即![]() . ②
. ②
由①②得![]() ,化簡得
,化簡得![]() . ③
. ③
焦點![]() 到直線
到直線![]() :
: ![]() 的距離
的距離 .
.
令![]() ,由
,由![]() 知
知![]() .
.
于是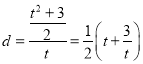 .
.
考慮到函數![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,解得
,解得![]() .
.


 名校課堂系列答案
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com