
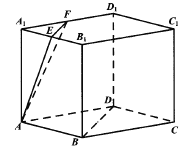
【題目】底面為菱形的直棱柱![]()
中, ![]()
分別為棱![]()
的中點(diǎn).
(1)在圖中作一個(gè)平面![]()
,使得![]()
,且平面![]()
.(不必給出證明過(guò)程,只要求作出![]()
與直棱柱![]()
的截面).
(2)若![]()
,求平面![]()
與平面![]()
的距離![]()
.
【答案】(1)見(jiàn)解析;(2)![]()
.
【解析】試題分析:(1)作面面平行,實(shí)質(zhì)作線線平行,而線線平行的尋找往往利用平幾知識(shí),如三角形中位線、平行四邊形性質(zhì)等,本題中已有![]()
,根據(jù)對(duì)稱性在平面![]()
中尋找另一組平行線,(2)利用向量投影可求兩平面之間距離,先根據(jù)條件建立恰當(dāng)直角坐標(biāo)系,設(shè)立各點(diǎn)坐標(biāo),解方程組得平面![]()
的法向量![]()
,利用向量數(shù)量積求向量![]()
在![]()
方向上投影的絕對(duì)值,即為平面![]()
與平面![]()
的距離![]()
.
試題解析:
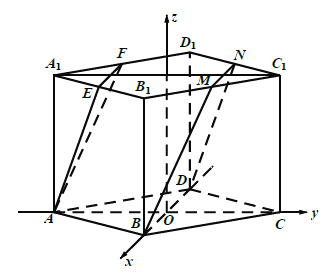
(1)如圖,取![]()
的中點(diǎn)![]()
,連接![]()
,則平面![]()
即為所求平面![]()
.
(2)如圖,連接![]()
交![]()
于![]()
,
∵在直棱柱![]()
中,底面為菱形,
∴![]()
,
∴分別以![]()
為![]()
軸, ![]()
為原點(diǎn)建立如圖所示空間直角坐標(biāo)系,
又∵所有棱長(zhǎng)為2, ![]()
,
∴![]()
, ![]()
, ![]()
,
∴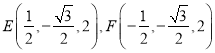
,
∴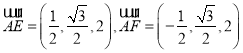
, ![]()
,
設(shè)![]()
是平面![]()
的一個(gè)法向量,則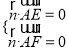
,即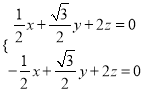
,
令![]()
得![]()
, ![]()
,
∴點(diǎn)![]()
到平面![]()
的距離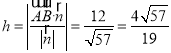
,
∴平面![]()
與平面![]()
的距離![]()
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司試銷一種成本單價(jià)為500元的新產(chǎn)品,規(guī)定試銷時(shí)銷售單價(jià)不低于成本單價(jià),又不高于800元.經(jīng)試銷調(diào)查,發(fā)現(xiàn)銷售量y(件)與銷售單價(jià)x(元)之間的關(guān)系可近似看作一次函數(shù)y=kx+b(k≠0),函數(shù)圖象如圖所示.

(1)根據(jù)圖象,求一次函數(shù)y=kx+b(k≠0)的表達(dá)式;
(2)設(shè)公司獲得的毛利潤(rùn)(毛利潤(rùn)=銷售總價(jià)-成本總價(jià))為S元.試問(wèn)銷售單價(jià)定為多少時(shí),該公司可獲得最大毛利潤(rùn)?最大毛利潤(rùn)是多少?此時(shí)的銷售量是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知某中學(xué)高三文科班學(xué)生共有800人參加了數(shù)學(xué)與地理的水平測(cè)試,現(xiàn)從中隨機(jī)抽取100人的數(shù)學(xué)與地理的水平測(cè)試成績(jī)?nèi)缦卤恚?/span>
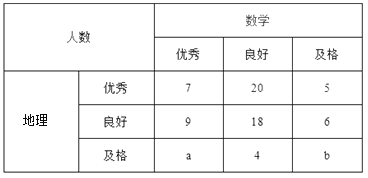
成績(jī)分為優(yōu)秀、良好、及格三個(gè)等級(jí);橫向,縱向分別表示地理成績(jī)與數(shù)學(xué)成績(jī),例如:表中數(shù)學(xué)成績(jī)?yōu)榱己玫墓灿?/span>![]() .
.
(Ⅰ)若在該樣本中,數(shù)學(xué)成績(jī)優(yōu)秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求數(shù)學(xué)成績(jī)?yōu)閮?yōu)秀的人數(shù)比及格的人數(shù)少的概率.
,求數(shù)學(xué)成績(jī)?yōu)閮?yōu)秀的人數(shù)比及格的人數(shù)少的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2016·桂林高二檢測(cè))如圖所示,在四邊形ABCD中,AB=AD=CD=1,BD=![]() ,BD⊥CD,將四邊形ABCD沿對(duì)角線BD折成四面體A′-BCD,使平面A′BD⊥平面BCD,則下列結(jié)論正確的是________.
,BD⊥CD,將四邊形ABCD沿對(duì)角線BD折成四面體A′-BCD,使平面A′BD⊥平面BCD,則下列結(jié)論正確的是________.

(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′與平面A′BD所成的角為30°.
(4)四面體A′-BCD的體積為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】【2014陜西理8】原命題為“若![]() 互為共軛復(fù)數(shù),則
互為共軛復(fù)數(shù),則![]() ”,關(guān)于逆命題,否命題,逆否命題真假性的判斷依次如下,正確的是( )
”,關(guān)于逆命題,否命題,逆否命題真假性的判斷依次如下,正確的是( )
A. 真,假,真 B. 假,假,真
C. 真,真,假 D. 假,假,假
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】經(jīng)過(guò)原點(diǎn)的直線與橢圓![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 為橢圓上不同于
為橢圓上不同于![]() 的一點(diǎn),直線
的一點(diǎn),直線![]() 的斜率均存在,且直線
的斜率均存在,且直線![]() 的斜率之積為
的斜率之積為![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)設(shè)![]() 分別為橢圓的左、右焦點(diǎn),斜率為
分別為橢圓的左、右焦點(diǎn),斜率為![]() 的直線
的直線![]() 經(jīng)過(guò)橢圓的右焦點(diǎn),且與橢圓交于
經(jīng)過(guò)橢圓的右焦點(diǎn),且與橢圓交于![]() 兩點(diǎn).若點(diǎn)
兩點(diǎn).若點(diǎn)![]() 在以
在以![]() 為直徑的圓內(nèi)部,求
為直徑的圓內(nèi)部,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|和a+b與c的夾角;
(2)設(shè)O為△ABC的外心,已知AB=3,AC=4,非零實(shí)數(shù)x,y滿足![]() =x
=x![]() +y
+y![]() ,且x+2y=1,求cos ∠BAC的值.
,且x+2y=1,求cos ∠BAC的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某漁場(chǎng)有一邊長(zhǎng)為20m的正三角形湖面ABC(如圖所示),計(jì)劃筑一條筆直的堤壩DE將水面分成面積相等的兩部分,以便進(jìn)行兩類水產(chǎn)品養(yǎng)殖試驗(yàn)(D在AB上,E在AC上).

(1)為了節(jié)約開(kāi)支,堤壩應(yīng)盡可能短,請(qǐng)問(wèn)該如何設(shè)計(jì)?堤壩最短為多少?
(2)將DE設(shè)計(jì)為景觀路線,堤壩應(yīng)盡可能長(zhǎng),請(qǐng)問(wèn)又該如何設(shè)計(jì)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商品的進(jìn)價(jià)為每件![]() 元,售價(jià)為每件
元,售價(jià)為每件![]() 元,每個(gè)月可賣出
元,每個(gè)月可賣出![]() 件;如果每件商品在該售價(jià)的基礎(chǔ)上每上漲
件;如果每件商品在該售價(jià)的基礎(chǔ)上每上漲![]() 元,則每個(gè)月少賣
元,則每個(gè)月少賣![]() 件(每件售價(jià)不能高于
件(每件售價(jià)不能高于![]() 元).設(shè)每件商品的售價(jià)上漲
元).設(shè)每件商品的售價(jià)上漲![]() 元(
元(![]() 為正整數(shù)),每個(gè)月的銷售利潤(rùn)為
為正整數(shù)),每個(gè)月的銷售利潤(rùn)為![]() 元.
元.
(1)求![]() 與
與![]() 的函數(shù)的函數(shù)關(guān)系式并直接寫(xiě)出自變量
的函數(shù)的函數(shù)關(guān)系式并直接寫(xiě)出自變量![]() 的取值范圍;
的取值范圍;
(2)每件商品的售價(jià)定為多少元時(shí),每個(gè)月可獲得最大利潤(rùn)?最大的月利潤(rùn)是多少元?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com