【題目】某校為了深入學習社會主義核心價值觀，對本校學生進行了一次相關知識的測試，隨機抽取了部分學生的測試成績進行統計（根據成績分為
、
、
、
、
五個組，
表示測試成績，組：
；組：
；組：
；組：
；組：
），通過對測試成績的分析，得到如圖所示的兩幅不完整的統計圖，請你根據圖中提供的信息解答以下問題：
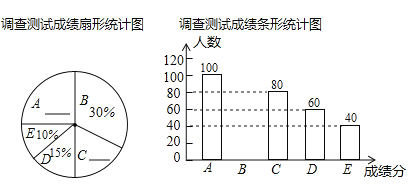
（1）抽取的學生共有______人，請將兩幅統計圖補充完整；
（2）抽取的測試成績的中位數落在______組內；
（3）本次測試成績在80分以上（含80分）為優秀，若該校初三學生共有1200人，請估計該校初三測試成績為優秀的學生有多少人？
【答案】（1）400，圖詳見解析；（2）B；（3）660人.
【解析】
（1）用E組的人數除以E組所占的百分比即可得出學生總人數；根據總人數乘以B組所占百分比可得B組的人數，利用A、C各組的人數除以總人數即得A、C兩組所占百分比，進而可補全兩幅統計圖；
（2）根據中位數的定義判斷即可；
（3）利用總人數乘以A、B兩組的百分比之和求解即可．
解：（1）40÷10%=400，∴抽取的學生共有400人；
B組人數為：400×30%=120，A組占：100÷400=25%，C組占：80÷400=20%，補全統計圖如下：
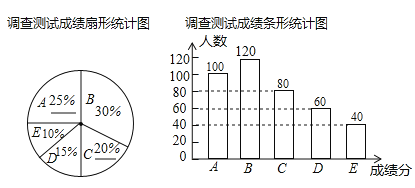
故答案為：400；
（2）∵A組有100人，B組有120人，C組有80人，D組有60人，E組有40人，
∴400的最中間的兩個數在B組，∴測試成績的中位數落在B組．
故答案為：B；
（3）1200×（25%+30%）＝660，∴該校初三測試成績為優秀的學生有660人．
科目：初中數學 來源： 題型：
【題目】下列3×3網格圖都是由9個相同的小正方形組成，每個網格圖中有3個小正方形已涂上陰影，請在余下的6個空白小正方形中，按下列要求涂上陰影：
(1)選取1個涂上陰影，使4個陰影小正方形組成一個軸對稱圖形，但不是中心對稱圖形；
(2)選取1個涂上陰影，使4個陰影小正方形組成一個中心對稱圖形，但不是軸對稱圖形；
(3)選取2個涂上陰影，使5個陰影小正方形組成一個軸對稱圖形．
(請將三個小題依次作答在圖1、圖2、圖3中，均只需畫出符合條件的一種情形)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝BC，以AB為直徑的⊙O與AC交于點D，過D作DF⊥BC， 交AB的延長線于E，垂足為F．
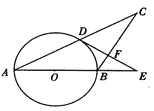
(1)求證：直線DE是⊙O的切線；
(2)當AB＝5，AC＝8時，求cosE的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】設二次函數y1＝ax2+bx+a﹣5（a，b為常數，a≠0），且2a+b＝3．
（1）若該二次函數的圖象過點（﹣1，4），求該二次函數的表達式；
（2）y1的圖象始終經過一個定點，若一次函數y2＝kx+b（k為常數，k≠0）的圖象也經過這個定點，探究實數k，a滿足的關系式；
（3）已知點P（x0，m）和Q（1，n）都在函數y1的圖象上，若x0＜1，且m＞n，求x0的取值范圍（用含a的代數式表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知拋物線
經過點
，對稱軸是直線
，頂點為點
，拋物線與
軸交于點
．
（1）求拋物線的表達式和點的坐標；
（2）將上述拋物線向下平移
個單位，平移后的拋物線與
軸正半軸交于點
，求
的面積；
（3）如果點
在原拋物線上，且在對稱軸的右側，聯結
交線段
于點
，
，求點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在x軸的上方，直角∠BOA繞原點O按順時針方向旋轉.若∠BOA的兩邊分別與函數
、
的圖象交于B、A兩點，則∠OAB大小的變化趨勢為（ ）
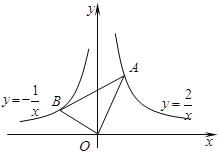
A.逐漸變小B.逐漸變大C.時大時小D.保持不變
查看答案和解析>>
科目：初中數學 來源： 題型：
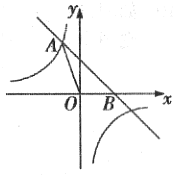
【題目】如圖，直線y=﹣x+2與反比例函數y=
的圖象相交于點A(a，3)，且與x軸相交于點B．
（1）求該反比例函數的表達式；
（2）寫出直線y=﹣x+2向下平移2個單位的直線解析式，并求出這條直線與雙曲線的交點坐標
查看答案和解析>>
科目：初中數學 來源： 題型：
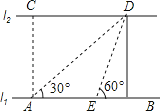
【題目】如圖，河的兩岸l1與l2互相平行，A、B是l1上的兩點，C、D是l2上的兩點，某同學在A處測得∠CAB＝90°，∠DAB＝30°，再沿AB方向走20米到達點E（即AE＝20），測得∠DEB＝60°.求：C，D兩點間的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
