
【題目】在![]() 中,以
中,以![]() 為斜邊,作直角
為斜邊,作直角![]() ,使點
,使點![]() 落在
落在![]() 內,
內,![]() .
.
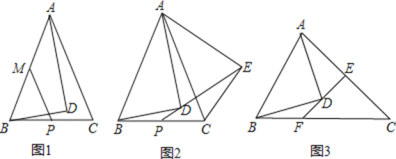
(1)如圖1,若![]() ,
,![]() ,
,![]() ,點,
,點,![]() 、
、![]() 分別為
分別為![]() ,
,![]() 的中點,連接
的中點,連接![]() ,求線段
,求線段![]() 的長;
的長;
(2)如圖2,若![]() ,把
,把![]() 繞點
繞點![]() 遞時針旋轉一定角度,得到
遞時針旋轉一定角度,得到![]() ,連接
,連接![]() 并延長變
并延長變![]() 于點
于點![]() ,求證:
,求證:![]() ;
;
(3)如圖3,若![]() ,過點
,過點![]() 的直線交
的直線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,
,![]() ,且
,且![]() ,請直接寫出線段
,請直接寫出線段![]() 、
、![]() 、
、![]() 之間的關系(不需要證明).
之間的關系(不需要證明).
【答案】(1)![]() (2)見解析,(3)
(2)見解析,(3)![]()
【解析】
(1)在直角三角形中,利用銳角三角函數求出AB,得到![]() 利用三角形中位線的性質即可得到答案;
利用三角形中位線的性質即可得到答案;
(2)先利用互余判斷出,∠BDP=∠PEC,得到△BDP和△CEQ全等,再用三角形的外角得到∠EPC=∠PQC,即可得到答案;
(3)連接AF,![]() 利用線段垂直平分線上的點到兩端點的距離相等,判斷出∠AFB=90°,利用勾股定理即可得到答案.
利用線段垂直平分線上的點到兩端點的距離相等,判斷出∠AFB=90°,利用勾股定理即可得到答案.
解:(1)∵∠ADB=90°,∠BAD=30°,![]() ,
,
∴cos∠BAD![]() ,
,
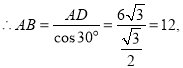
∴AC=AB=12,
∵點P、M分別為BC、AB邊的中點,
∴PM=![]() AC=6,
AC=6,
(2)如圖2,
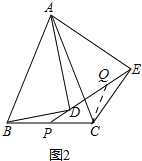
在ED上截取EQ=PD,
∵∠ADB=90°,
∴∠BDP+∠ADE=90°,
∵AD=AE,
∴∠ADE=∠AED,
∵把△ABD繞點A逆時針旋轉一定角度,得到△ACE,
∴∠AEC=∠ADB=90°
∵∠AED+∠PEC=90°,
∴∠BDP=∠PEC,
在△BDP和△CEQ中,
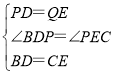 ,
,
∴△BDP≌△CEQ,
∴BP=CQ,∠DBP=∠QCE,
∵∠CPE=∠BDP+∠DBP,
∠PQC=∠PEC+∠QCE,
∴∠EPC=∠PQC,
∴PC=CQ,
∴BP=CP
(3)![]()
理由:如圖3,
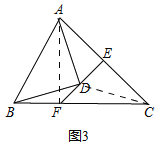
連接AF,![]()
∵EF⊥AC,且AE=EC,
∴FA=FC,∠FAC=∠FCA,
∵EF⊥AC,且AE=EC,
∴∠DAC=∠DCA,DA=DC,
∵AD=BD,
∴BD=DC,
∴∠DBC=∠DCB,
∵∠FAC=∠FCA,∠DAC=∠DCA,
∴∠DAF=∠DCB,
∴∠DAF=∠DBC,
∴∠AFB=∠ADB=90°,
在Rt△ADB中,DA=DB,
∴![]()
在Rt△ABF中,![]()
∵FA=FC
∴![]()


科目:初中數學 來源: 題型:
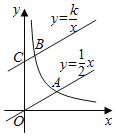
【題目】如圖,直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0,x>0)交于點A,將直線y=
(k>0,x>0)交于點A,將直線y=![]() x向上平移2個單位長度后,與y軸交于點C,與雙曲線交于點B,若OA=3BC,則k的值為____.
x向上平移2個單位長度后,與y軸交于點C,與雙曲線交于點B,若OA=3BC,則k的值為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[閱讀理解]
我們知道:![]() ,那么
,那么![]() 結果等于多少呢?
結果等于多少呢?
在圖1所示的等邊三角形數陣中,第![]() 行的一個小等邊三角形中的數為
行的一個小等邊三角形中的數為![]() ,即
,即![]() 第
第![]() 行的三個小等邊三角形中的數的和是
行的三個小等邊三角形中的數的和是![]() 即
即![]() ; ..第
; ..第![]() 行的
行的![]() 個小等邊三角形中的數的和是
個小等邊三角形中的數的和是![]() 個,即
個,即![]() ,該等邊三角形數陣中共有
,該等邊三角形數陣中共有![]() 小等邊三角形,所有小等邊三角形數的和為
小等邊三角形,所有小等邊三角形數的和為![]() .
.
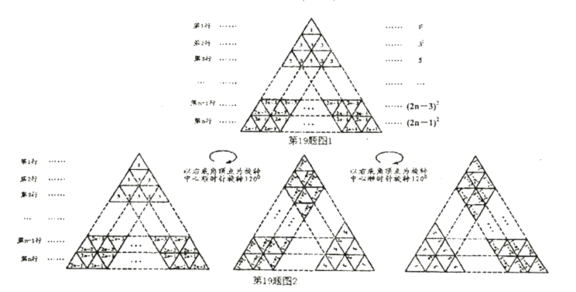
[規律探究]
以圖1中的等邊三角形數陣的右底角頂點為旋轉中心順時針旋轉![]() 再把旋轉后的圖形按同樣的方法可得如圖2所示的三角形數陣,觀察這三個等邊三角形數陣各行同一位置的小等邊三角形中的數,發現位于奇數位置的三個數(如第
再把旋轉后的圖形按同樣的方法可得如圖2所示的三角形數陣,觀察這三個等邊三角形數陣各行同一位置的小等邊三角形中的數,發現位于奇數位置的三個數(如第![]() 行的第
行的第![]() 個小三角形中的數分別為
個小三角形中的數分別為![]() 的和為
的和為![]() ;發現位于偶數位置的三個數(如第
;發現位于偶數位置的三個數(如第![]() 行的第
行的第![]() 個小三角形中的數分別為
個小三角形中的數分別為![]() 的和為
的和為![]() ;而每個等邊三角形數陣中,由于位于奇數位置的數比位于偶數位置的數多
;而每個等邊三角形數陣中,由于位于奇數位置的數比位于偶數位置的數多![]() 個,則位于偶數位置的數有_
個,則位于偶數位置的數有_
個![]()
因此,![]()
[解決問題]根據以上發現,計算:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于二次函數![]() ,下列說法正確的個數是( )
,下列說法正確的個數是( )
①對于任何滿足條件的![]() ,該二次函數的圖象都經過點
,該二次函數的圖象都經過點![]() 和
和![]() 兩點;
兩點;
②若該函數圖象的對稱軸為直線![]() ,則必有
,則必有![]() ;
;
③當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
④若![]() ,
,![]() 是函數圖象上的兩點,如果
是函數圖象上的兩點,如果![]() 總成立,則
總成立,則![]() .
.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,
上,![]() 是
是![]() 的切線,
的切線,![]() 于點
于點![]() ,
,![]() 是
是![]() 延長線上一點,
延長線上一點,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.

(1)求證:![]() 平分
平分![]() ;
;
(2)若![]() ,
,![]() ,
,
①求![]() 的度數;
的度數;
②若![]() 的半徑為2,求線段
的半徑為2,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在正方形ABCD中,G為CD邊中點,連接AG并延長交BC邊的延長線于E點,對角線BD交AG于F點.已知FG=2,則線段AE的長度為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,M,N分別為銳角∠AOB的邊OA,OB上的點,ON=6,把△OMN沿MN折疊,點O落在點C處,MC與OB交于點P,若MN=MP=5,則PN=( )
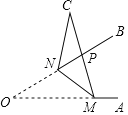
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校對交通法則的了解情況在全校隨機調查了部分學生,調查結果分為四種:![]() .非常了解,
.非常了解,![]() .比較了解,
.比較了解,![]() .基本了解,
.基本了解,![]() .不太了解,并將此次調查結果整理繪制成下面不完整的條形統計圖和扇形統計圖.
.不太了解,并將此次調查結果整理繪制成下面不完整的條形統計圖和扇形統計圖.
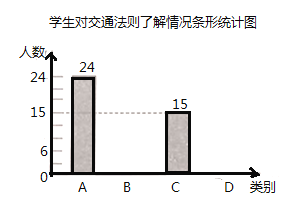
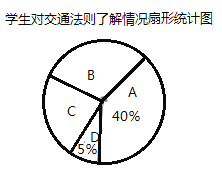
(1)本次共調查_______名學生;扇形統計圖中![]() 所對應扇形的圓心角度數是_______;
所對應扇形的圓心角度數是_______;
(2)補全條形統計圖;
(3)學校準備從甲、乙、丙、丁四位學生中隨機抽取兩名學生參加市區交通法規競賽,請用列表或畫樹狀圖的方法求甲和乙兩名學生同時被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級10個班的300名學生即將參加學校舉行的研究旅行活動,學校提出以下4個活動主題:A.赤水丹霞地貌考察;B.平塘天文知識考察;C.山關紅色文化考察;D.海龍電土司文化考察,為了解學生喜歡的活動主題,學生會開展了一次調查研究,請將下面的過程補全
(1)收集數據:學生會計劃調查學生喜歡的活動主題情況,下面抽樣調查的對象選擇合理的是______.(填序號)
①選擇七年級3班、4班、5班學生作為調查對象
②選擇學校旅游攝影社團的學生作為調查對象
③選擇各班學號為6的倍數的學生作為調查對象
(2)整理、描述數據:通過調査后,學生會同學繪制了如下兩幅不完整的統計圖,請把統計圖補充完整
某校七年級學生喜歡的活動主題條形統計圖某校七年級學生喜歡的活動主題扇形統計圖
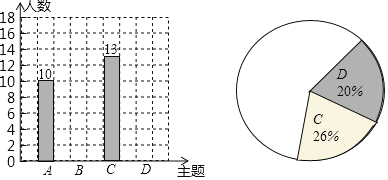
(3)分析數據、推斷結論:請你根據上述調查結果向學校推薦本次活動的主題,你的推薦是______(填A-D的字母代號),估算全年級大約有多少名學生喜歡這個主題活動
(4)若在5名學生會干部(3男2女)中,隨機選取2名同學擔任活動的組長和副組長,求抽出的兩名同學恰好是1男1女的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com