
【題目】如圖,在矩形ABCD中,AB=3,BC=4,動點P以每秒一個單位的速度從點A出發,沿對角線AC向點C移動,同時動點Q以相同的速度從點C出發,沿邊CB向點B移動.設P,Q兩點移動時間為t秒(0≤t≤4).
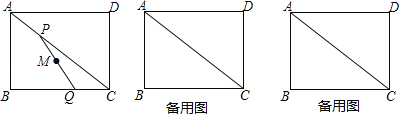
(1)用含t的代數式表示線段PC的長是 ;
(2)當△PCQ為等腰三角形時,求t的值;
(3)以BQ為直徑的圓交PQ于點M,當M為PQ的中點時,求t的值.
【答案】(1)5﹣t;(2)當t=![]() 或t=
或t=![]() 或t=
或t=![]() 時,△PCQ為等腰三角形;(3)當M為PQ的中點時,t的值為
時,△PCQ為等腰三角形;(3)當M為PQ的中點時,t的值為![]() .
.
【解析】
試題分析:(1)根據勾股定理求出AC,根據題意用t表示出AP,結合圖形計算即可;
(2)分CP=CQ、QP=QC、PQ=PC三種情況,根據等腰三角形的性質和相似三角形的判定和性質計算即可;
(3)連接BP、BM,根據直徑所對的圓周角是直角、等腰三角形的三線合一得到BP=BQ,根據勾股定理用t表示出BP、BQ,列出方程,解方程即可.
解:(1)∵∠B=90°,AB=3,BC=4,
∴AC=5,
∵點P的速度是每秒一個單位,移動時間為t秒,
∴AP=t,
則PC=AC﹣AP=5﹣t,
故答案為:5﹣t;
(2)當CP=CQ時,t=5﹣t,
解得t=![]() ,
,
當QP=QC時,過點Q作QH⊥AC于H,如圖1,
則PH=HC=![]() PC=
PC=![]() (5﹣t),QC=t,
(5﹣t),QC=t,
∵QH⊥AC,∠B=90°,
∴△CHQ∽△CBA,
∴![]() =
=![]() ,即
,即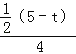 =
=![]() ,
,
解得t=![]() ,
,
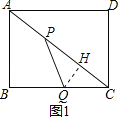
當PQ=PC時,如圖2,
過點P作PN⊥QC于N,
則NC=NQ=![]() QC=
QC=![]() t,
t,
∵△CPN∽△CAB,得
![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() ,
,
綜上所述,當t=![]() 或t=
或t=![]() 或t=
或t=![]() 時,△PCQ為等腰三角形;
時,△PCQ為等腰三角形;
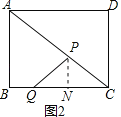
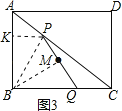
(3)連接BP、BM,如圖3,則∠BMQ=90°,
∵M為PQ的中點,
∴BP=BQ,
過點P作PK⊥AB于K,
∵AP=t,
∴PK=![]() t,AK=
t,AK=![]() t,
t,
∴BK=3﹣![]() t,
t,
在Rt△BPK中,PB2=PK2+BK2=(3﹣![]() t)2+(
t)2+(![]() t)2,又BQ=4﹣t,
t)2,又BQ=4﹣t,
∴(4﹣t)2=(3﹣![]() t)2+(
t)2+(![]() t)2,
t)2,
解得t=![]() .
.
∴以BQ為直徑的圓交PQ于點M,當M為PQ的中點時,t的值為![]() .
.


科目:初中數學 來源: 題型:
【題目】一個正方形的邊長為5 cm,它的邊長減少x(cm)后得到的新正方形的周長為y(cm).
(1)求y關于x的函數表達式.
(2)當x=2時,求y的值,并說明這個函數值的實際意義.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2﹣2x﹣3與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,該拋物線頂點為D,對稱軸交x軸于點H.
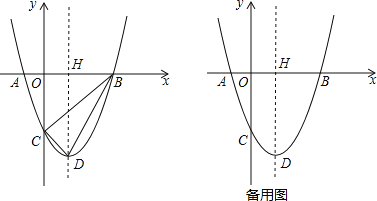
(1)求A,B兩點的坐標;
(2)設點P在x軸下方的拋物線上,當∠ABP=∠CDB時,求出點P的坐標;
(3)以OB為邊最第四象限內作等邊△OBM.設點E為x軸的正半軸上一動點(OE>OH),連接ME,把線段ME繞點M順時針旋轉60°得MF,求線段DF的長的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小宋作出了邊長為2的第一個正方形A1B1C1D1,算出了它的面積.然后分別取正方形A1B1C1D1四邊的中點A2、B2、C2、D2作出了第二個正方形A2B2C2D2,算出了它的面積.用同樣的方法,作出了第三個正方形A3B3C3D3,算出了它的面積…,由此可得,第六個正方形A6B6C6D6的面積是( )
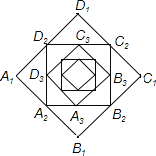
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2011年長江中下游地區發生了特大旱情.為抗旱保豐收,某地政府制定了農戶投資購買抗旱設備的補貼辦法,其中購買Ⅰ型、Ⅱ型抗旱設備投資的金額與政府補的額度存在下表所示的函數對應關系.

(1)分別求y1和y2的函數解析式;
(2)有一農戶同時對Ⅰ型、Ⅱ型兩種設備共投資10萬元購買,請你設計一個能獲得最大補貼金額的方案,并求出按此方案能獲得的最大補貼金額.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com