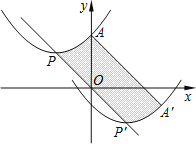
【題目】如圖，拋物線的頂點為
，與y軸交于點
若平移該拋物線使其頂點P沿直線移動到點
，點A的對應點為
，則拋物線上PA段掃過的區域
陰影部分
的面積為______．
科目：初中數學 來源： 題型：
【題目】完成下面的證明．
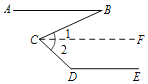
已知：如圖，AB∥DE，求證：∠D+∠BCD﹣∠B＝180°．
證明：過點C作CF∥AB．
∵CF∥AB（已作），
∴∠1＝ ．
∵∠2＝∠BCD﹣∠1，
∴∠2＝∠BCD﹣∠B ．
∵AB∥DE，CF∥AB（已知），
∴CF∥DE
∴∠D+∠2＝180°
∴∠D+∠BCD﹣∠B＝180° ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，A(a，0)，B(0，b)，C（-a，0），且
+b2-4b+4=0．
(1)求證：∠ABC=90°；
(2)∠ABO的平分線交x軸于點D，求D點的坐標．
(3)如圖，在線段AB上有兩動點M、N滿足∠MON=45°，求證：BM2+AN2=MN2．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某辦公樓AB的后面有一建筑物CD，當光線與地面的夾角是22°時，辦公樓在建筑物的墻上留下高3米的影子CE，而當光線與地面夾角是45°時，辦公樓頂A在地面上的影子F與墻角C有27米的距離（B，F，C在一條直線上）．
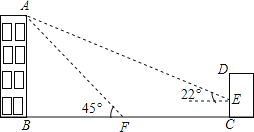
（1）求辦公樓AB的高度；
（2）若要在A，E之間掛一些彩旗，請你求出A，E之間的距離．
（參考數據：sin22°≈
，cos22°≈
，tan22°≈
）
查看答案和解析>>
科目：初中數學 來源： 題型：
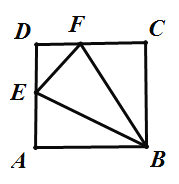
【題目】如圖，已知長方形ABCD，點E在線段AD上，將
沿直線BE翻折后，點A落在線段CD上的點F.如果
的周長為12，
的周長為24，那么FC長為________.
查看答案和解析>>
科目：初中數學 來源： 題型：
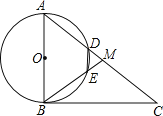
【題目】如圖，在
中，
，點M是AC的中點，以AB為直徑作
分別交
于點
．
求證：
；
填空：
若
，當
時，
______；
連接
，當
的度數為______時，四邊形ODME是菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】高斯上小學時，有一次數學老師讓同學們計算“從1到100這100個正整數的和”．許多同學都采用了依次累加的計算方法，計算起來非常繁瑣，且易出錯．聰明的小高斯經過探索后，給出了下面漂亮的解答過程．
解：設S＝1+2+3+…+100 ①
則S＝100+99+98+…+1 ②
①+②，得（即左右兩邊分別相加）：
2S＝（1+100）+（2+99）+（3+98）+…+（100+1），
＝
，
＝100×101，
所以，S＝
③，
所以，1+2+3+…+100＝5050．
后來人們將小高斯的這種解答方法概括為“倒序相加法”．請你利用“倒序相加法”解答下面的問題．
（1）計算：1+2+3+…+101；
（2）請你觀察上面解答過程中的③式及你運算過程中出現的類似③式，猜想：1+2+3+…+n＝ ；
（3）至少用兩種方法計算：1001+1002+…+2000．
方法1：
方法2：
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，函數y=
的圖象與雙曲線y=
(k≠0，x>0)相交于點A(3，m)和點B．
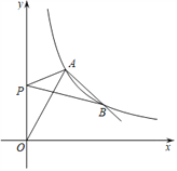
（1）求雙曲線的解析式及點B的坐標；
（2）若點P在y軸上，連接PA，PB，求當PA+PB的值最小時點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，直線l1：
與坐標軸交于A，B兩點，直線l2：
（
≠0）與坐標軸交于點C，D.
（1）求點A，B的坐標；
（2）如圖，當=2時，直線l1，l2與相交于點E，求兩條直線與
軸圍成的△BDE的面積；
（3）若直線l1，l2與軸不能圍成三角形，點P（a，b）在直線l2：（k≠0）上，且點P在第一象限.
①求的值；
②若
,，求
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
