
【題目】如圖,已知二次函數![]() 圖象過點
圖象過點![]() ,頂點為
,頂點為![]() ,則結論:①
,則結論:①![]() ;②
;②![]() 時,函數的最大值是
時,函數的最大值是![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正確的結論有( )
.其中正確的結論有( )
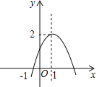
A. 1個 B. 2個 C. 3個 D. 4個
【答案】C
【解析】
由拋物線開口方向得到a<0,由拋物線的對稱軸為直線x=-![]() =1,則b=-2a>0,由拋物線與y軸的交點在x軸上方得c>0,則可對①進行判斷;
=1,則b=-2a>0,由拋物線與y軸的交點在x軸上方得c>0,則可對①進行判斷;
由于拋物線的頂點坐標為(1,2),根據二次函數的性質可對②進行判斷;
由于x=![]() 時,y>0,即
時,y>0,即![]() a+
a+![]() b+c>0,則a+2b+4c>0,于是可對③進行判斷;
b+c>0,則a+2b+4c>0,于是可對③進行判斷;
根據拋物線的對稱軸為直線x=-![]() =1可得2a=-b,所以可對④進行判斷;
=1可得2a=-b,所以可對④進行判斷;
利用拋物線過點(-1,0)得到a-b+c=0,而a=-![]() b,則-
b,則-![]() b-b+c=0,變形得到2c=3b,則可對⑤進行判斷.
b-b+c=0,變形得到2c=3b,則可對⑤進行判斷.
解:∵拋物線開口向下,
∴a<0,
∵拋物線的對稱軸為直線x=-![]() =1,
=1,
∴b=-2a>0,
∵拋物線與y軸的交點在x軸上方,
∴c>0,
∴abc<0,所以①正確;
∵拋物線的頂點坐標為(1,2),
∴x=1時,函數有大值2,所以②正確;
∵x=![]() 時,y>0,即
時,y>0,即![]() a+
a+![]() b+c>0,
b+c>0,
∴a+2b+4c>0,所以③錯誤;
∵拋物線的對稱軸為直線x=-![]() =1,
=1,
∴2a=-b,所以④正確;
∵拋物線過點(-1,0),
∴a-b+c=0,
而a=-![]() b,
b,
∴-![]() b-b+c=0,
b-b+c=0,
∴2c=3b,所以⑤錯誤.
故選:C.


 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】對x,y定義一種新運算T,規定T(x,y)=![]() (其中a,b是非零常數,且x+y≠0),這里等式右邊是通常的四則運算.
(其中a,b是非零常數,且x+y≠0),這里等式右邊是通常的四則運算.
如:T(3,1)=![]() ,T(m,﹣2)=
,T(m,﹣2)=![]() .
.
(1)填空:T(4,﹣1)= (用含a,b的代數式表示);
(2)若T(﹣2,0)=﹣2且T(5,﹣1)=6.
①求a與b的值;
②若T(3m﹣10,m)=T(m,3m﹣10),求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“我們應該討論一般化、特殊化和類比這些過程本身,他們是獲得發現的偉大源泉”——喬治·波利亞.
(1)觀察猜想
如圖1,在△ABC中,CA=CB,![]() .點D在AC上,點E在BC上,且CD=CE.則BE與AD的數量關系是______,直線BE與直線AD的位置關系是______;
.點D在AC上,點E在BC上,且CD=CE.則BE與AD的數量關系是______,直線BE與直線AD的位置關系是______;
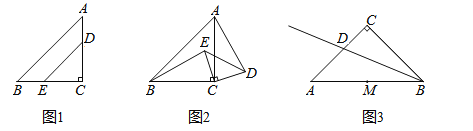
(2)拓展探究
如圖2,在△ABC和△CDE中,CA=CB,CD=CE,![]() .則BE與AD的數量關系怎樣?直線BE與直線AD的位置關系怎樣?請說明理由;
.則BE與AD的數量關系怎樣?直線BE與直線AD的位置關系怎樣?請說明理由;
(3)解決問題
如圖3,在△ABC中,CA=CB,![]() ,BD是△ABC的角平分線,點M是AB的中點.點P在射線BD上,連接PM,以點M為中心,將PM逆時針旋轉90°,得到線段MN,請直接寫出點A,P,N在同一條直線上時
,BD是△ABC的角平分線,點M是AB的中點.點P在射線BD上,連接PM,以點M為中心,將PM逆時針旋轉90°,得到線段MN,請直接寫出點A,P,N在同一條直線上時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,直線PQ垂直平分AC,與邊AB交于E,連接CE,過點C作CF平行于BA交PQ于點F,連接AF.
(1)求證:△AED≌△CFD;
(2)求證:四邊形AECF是菱形.
(3)若AD=3,AE=5,則菱形AECF的面積是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象如圖所示,有下列
的圖象如圖所示,有下列![]() 個結論:
個結論:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() (
(![]() 的實數);⑥
的實數);⑥![]()
其中正確的結論有( )
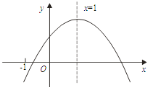
A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC內接于⊙O,AC是⊙O的直徑,D是![]() 的中點.過點D作CB的垂線,分別交CB、CA延長線于點F、E.
的中點.過點D作CB的垂線,分別交CB、CA延長線于點F、E. 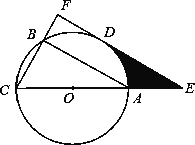
(1)判斷直線EF與⊙O的位置關系,并說明理由;
(2)若CF=6,∠ACB=60°,求陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
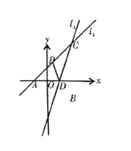
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 相交于點
相交于點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)在![]() 軸上一點
軸上一點![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)直線![]() 上一點
上一點![]() ,平面內一點
,平面內一點![]() ,若以
,若以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 全等,求點
全等,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com