
【題目】已知△ABC中,∠ACB=90°,CD、CE分別是中線和角平分線,當∠A= °時,△CDE是等腰三角形.
【答案】15或75.
【解析】
試題分析:有兩種情況:①中線CD在角平分線CE的左邊,由直角三角形斜邊中線定理可以知道△BCD是等腰三角形,△CDE要是等腰三角形只有一種情況,即CE=DE,∠DCE=∠CDE,由外角定理可以知道∠CDE=∠B+∠BCD=2∠BCD,又因為∠CDE=∠DCE,且∠DCE+∠BCD=45°,所以3∠BCD=3∠B=45°,∠B=15°,∠A=90°-∠B=75°;
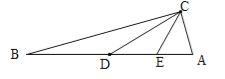
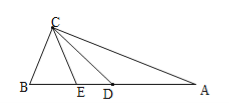
②中線CD在角平分線CE的右邊,由直角三角形斜邊中線定理可以知道△ACD是等腰三角形,△CDE要是等腰三角形只有一種情況,即CE=DE,∠DCE=∠CDE,由外角定理可以知道∠CDE=∠A+∠ACD=2∠ACD,又因為∠CDE=∠DCE,且∠DCE+∠ACD=45°,所以3∠ACD=3∠A=45°,∠A=15°;故答案為:15或75.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】某地的一座人行天橋如圖所示,天橋高為6米,坡面BC的坡度為1:1,為了方便行人推車過天橋,有關部門決定降低坡度,使新坡面的坡度為1:![]() .
.
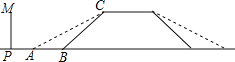
(1)求新坡面的坡角a;
(2)原天橋底部正前方8米處(PB的長)的文化墻PM是否需要拆橋?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一種藥品原價每盒25元,經過兩次降價后每盒16元,兩次降價的百分率相同,設每次降價的百分率為x,則符合題意的方程為( )
A. 16(1+2x)=25 B. 25(1﹣2x)=16 C. 16(1+x)2=25 D. 25(1﹣x)2=16
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com