
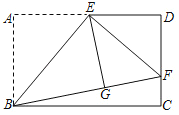
【題目】如圖,矩形ABCD中,E是AD的中點,將△ABE沿BE折疊使點A落在點G處,延長BG交CD于點F,連接EF,若CF=1,DF=2,則BC的長是( )
A.3![]() B.
B.![]() C.5D.2
C.5D.2![]()
【答案】D
【解析】
首先過點E作EM⊥BC于M,交BF于N,易證得△ENG≌△BNM(AAS),MN是△BCF的中位線,根據全等三角形的性質,即可求得GN=MN,由折疊的性質,可得BG=3,繼而求得BF的值,又由勾股定理,即可求得BC的長.
解:過點E作EM⊥BC于M,交BF于N,
∵四邊形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°, ∴四邊形ABME是矩形,
∴AE=BM, 由折疊的性質得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
∵∠ENG=∠BNM,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∵E是AD的中點, ∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM=![]() CF=
CF=![]() ,
,
∴NG=![]() ,
,
∵BG=AB=CD=CF+DF=3,
∴BN=BG-NG=3-![]() =
=![]() ,
,
∴BF=2BN=5,
∴BC=![]()
故選:D.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:初中數學 來源: 題型:
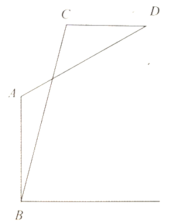
【題目】無影塔位于河南汝南城南,俗傳冬至正午無塔影,故稱無影塔;相傳為唐代和尚悟顆所建,故又稱“悟穎塔”,該塔應建于北宋中、早期,為豫南地區現存最古之磚塔.某數學小組為了度量塔高進行了如下操作:用一架無人機在距離塔基![]() 8米處垂直起飛30米至點
8米處垂直起飛30米至點![]() 處,測得塔基
處,測得塔基![]() 處的俯角為
處的俯角為![]() ,將無人機沿水平方向向右飛行
,將無人機沿水平方向向右飛行![]() 米至點
米至點![]() ,在此處測得塔頂
,在此處測得塔頂![]() 的俯角為
的俯角為![]() ,請依據題中數據計算無影塔的高度.(結果精確到
,請依據題中數據計算無影塔的高度.(結果精確到![]() ,參考數據:
,參考數據:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某初中課外興趣活動小組對某水稻品種的稻穗谷粒數目進行調查,從試驗田中隨機抽取了30株,得到的數據如下(單位:顆):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)對抽取的30株水稻稻穗谷粒數進行統計分析,請補全下表中空格,并完善直方圖:
谷粒顆數 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
頻數 | 8 | 10 | 3 | ||
對應扇形 圖中區域 | D | E | C |

(2)如圖所示的扇形統計圖中,扇形A對應的圓心角為 度,扇形B對應的圓心角為 度;
(3)該試驗田中大約有3000株水稻,據此估計,其中稻穗谷粒數大于或等于205顆的水稻有多少株?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,A,B兩個頂點在x軸上方,點C的坐標是(﹣1,0),以點C為位似中心,在x軸的下方作△ABC的位似圖形,并把△ABC的邊長放大到原來的2倍,得到△A'B'C',設點B的對應點B'的橫坐標為2,則點B的橫坐標為( )
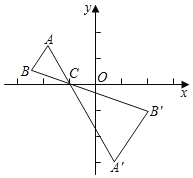
A.﹣1B.![]() C.﹣2D.
C.﹣2D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,以AB為直徑的⊙O交BC于點E,且點E是![]() 的中點,連接AD交BE于點F,連接EA,ED.
的中點,連接AD交BE于點F,連接EA,ED.
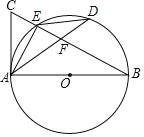
(1)求證:AC=AF;
(2)若EF=2,BF=8,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地為了了解2020年在疫情中上網課的感受,組織教師通過問卷和座談等形式,隨機抽取某城區一些初中學生進行調查,并將調查的普遍感受分為四大類:A.提高自律能力;B.戰親子關系;C.提升信息素養;D.教師敬業辛苦,并將調查結果繪制成頻數折線統計圖1和扇形統計圖2(不完整).請根據圖中提供的信息,解答下列問題:
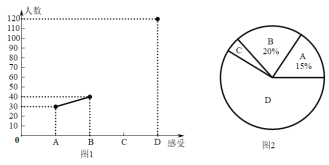
(1)此次抽樣調查中,共調查了__________名初中學生;
(2)求出圖2中扇形C所對的圓心角的度數,并將圖1補充完整;
(3)根據抽樣調查結果,請你估計該城區1000名初中學生中有多少人的感受是“教師敬業辛苦”?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 軸的正半軸上,頂點
軸的正半軸上,頂點![]() 的坐標為
的坐標為![]() .點
.點![]() 是邊
是邊![]() 上的一個動點(不與
上的一個動點(不與![]() 、
、![]() 重合),反比例函數
重合),反比例函數![]()
![]() 的圖象經過點
的圖象經過點![]() 且與邊
且與邊![]() 交于點
交于點![]() ,連接
,連接![]() .
.
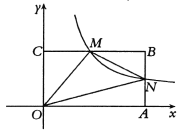
(1)當點![]() 是邊
是邊![]() 的中點時,求反比例函數的表達式
的中點時,求反比例函數的表達式
(2)在點![]() 的運動過程中,試證明:
的運動過程中,試證明:![]() 是一個定值.
是一個定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,為放置在水平桌面![]() 上的臺燈,底座的高
上的臺燈,底座的高![]() 為
為![]() .長度均為
.長度均為![]() 的連桿
的連桿![]() ,
,![]() 與
與![]() 始終在同一水平面上.
始終在同一水平面上.
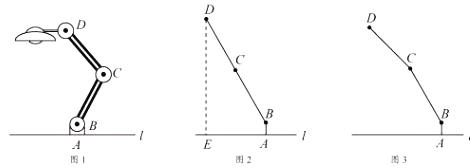
(1)旋轉連桿![]() ,
,![]() ,使
,使![]() 成平角,
成平角,![]() ,如圖2,求連桿端點
,如圖2,求連桿端點![]() 離桌面
離桌面![]() 的高度
的高度![]() .
.
(2)將(1)中的連桿![]() 繞點
繞點![]() 逆時針旋轉,使
逆時針旋轉,使![]() ,如圖3,問此時連桿端點
,如圖3,問此時連桿端點![]() 離桌面
離桌面![]() 的高度是增加了還是減少?增加或減少了多少?(精確到
的高度是增加了還是減少?增加或減少了多少?(精確到![]() ,參考數據:
,參考數據:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com