
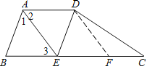
【題目】如圖所示,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.

![]() 求證:四邊形
求證:四邊形![]() 是菱形;
是菱形;
![]() 若
若![]() ,
,![]() ,試判斷
,試判斷![]() 的形狀,并說明理由.
的形狀,并說明理由.
【答案】(1)見解析;(2)見解析.
【解析】
根據(jù)已知條件易證![]() ,由全等三角形的性質(zhì)可得BE=DE,再由平行線的性質(zhì)可得
,由全等三角形的性質(zhì)可得BE=DE,再由平行線的性質(zhì)可得![]() ,即可證得
,即可證得![]() ,根據(jù)四條邊相等的四邊形是菱形即可判定四邊形
,根據(jù)四條邊相等的四邊形是菱形即可判定四邊形![]() 是菱形;(2)
是菱形;(2)![]() 是直角三角形.如圖,過點
是直角三角形.如圖,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,即可得四邊形AEFD是平行四邊形,所以DF=AE,AD=EF=BE,再由CE=2BE得出DE=EF,再判定
,即可得四邊形AEFD是平行四邊形,所以DF=AE,AD=EF=BE,再由CE=2BE得出DE=EF,再判定![]() 是等邊三角形,即可得
是等邊三角形,即可得![]() ,由此證得結論.
,由此證得結論.
![]() 證明:如圖,∵
證明:如圖,∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四邊形![]() 是菱形.
是菱形.
![]() 是直角三角形.
是直角三角形.
如圖,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,
,
∵![]() ,
,![]()
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,
∴![]() 是直角三角形.
是直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
【題目】如果一條拋物線y=ax2+bx+c(a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.在拋物線y=ax2+bx+c中,系數(shù)a、b、c為絕對值不大于1的整數(shù),則該拋物線的“拋物線三角形”是等腰直角三角形的概率為_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
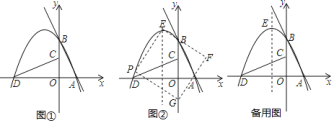
【題目】如圖①,若直線![]() 交
交![]() 軸于點
軸于點![]() 、交
、交![]() 軸于點
軸于點![]() ,將
,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() .過點
.過點![]() ,
,![]() ,
,![]() 的拋物線
的拋物線![]() .
.
![]() 求拋物線
求拋物線![]() 的表達式;
的表達式;
![]() 若與
若與![]() 軸平行的直線
軸平行的直線![]() 以
以![]() 秒鐘一個單位長的速度從
秒鐘一個單位長的速度從![]() 軸向左平移,交線段
軸向左平移,交線段![]() 于點
于點![]() 、交拋物線
、交拋物線![]() 于點
于點![]() ,求線段
,求線段![]() 的最大值;
的最大值;
![]() 如圖②,點
如圖②,點![]() 為拋物線
為拋物線![]() 的頂點,點
的頂點,點![]() 是拋物線
是拋物線![]() 在第二象限的上一動點(不與點
在第二象限的上一動點(不與點![]() 、
、![]() 重合),連接
重合),連接![]() ,以
,以![]() 為邊作圖示一側的正方形
為邊作圖示一側的正方形![]() .隨著點
.隨著點![]() 的運動,正方形的大小、位置也隨之改變,當頂點
的運動,正方形的大小、位置也隨之改變,當頂點![]() 或
或![]() 恰好落在
恰好落在![]() 軸上時,直接寫出對應的點
軸上時,直接寫出對應的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,小華剪了兩條寬為1的紙條,交叉疊放在一起,且它們較小的交角為60°,則它們重疊部分的面積為( )

A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
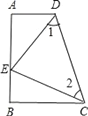
【題目】如圖,四邊形ABCD中,∠A=∠B=90°,E是AB上一點,且AE=BC,∠1=∠2.
(1)證明:AB=AD+BC;
(2)判斷△CDE的形狀?并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
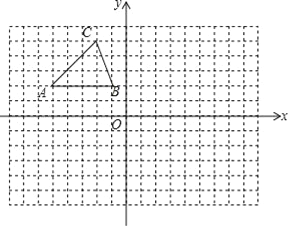
【題目】在如圖的方格中,每個小正方形的邊長都為1,△ABC的頂點均在格點上.在建立平面直角坐標系后,點B的坐標為(﹣1,2).
(1)把△ABC向下平移8個單位后得到對應的△A1B1C1,畫出△A1B1C1;
(2)畫出與△A1B1C1關于y軸對稱的△A2B2C2;
(3)若點P(a,b)是△ABC邊上任意一點,P2是△A2B2C2邊上與P對應的點,寫出P2的坐標為 ;
(4)試在y軸上找一點Q(在圖中標出來),使得點Q到B2、C2兩點的距離之和最小,并求出QB2+QC2的最小值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,CE⊥AD于點E,且CB=CE,點F為CD邊上的一點,CB=CF,連接BF交CE于點G.
(1)若∠D=60°,CF=2![]() ,求CG的長度;
,求CG的長度;
(2)求證:AB=ED+CG.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com