【題目】在平面直角坐標系中，己知
為等腰三角形且面積為
,滿足條件的
點有( )
A.
個B.
個C.
個D.
個
【答案】D
【解析】
先利用
的面積是9，求得OM邊上的高為3，然后分三種情況：①當OM=MN時，②當OM=ON時，③當MN=ON時，分別求得點N的個數，即可得到答案.
∵
，
∴OM=6，
設中，OM邊上的高為h，
∴
，解得h=3，
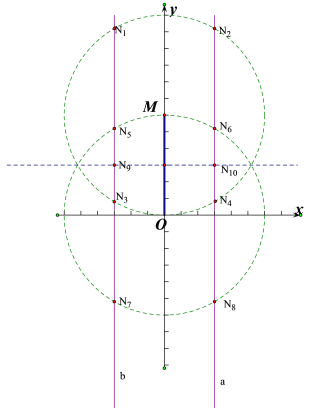
在y軸的兩側作直線a和直線b都和y軸平行，且到y軸的距離都等于3，如圖，
①當OM=MN時，
以點M為圓心，以3為半徑畫圓，交直線a和直線b分別有2個點，即有4個點符合；
②當OM=ON時，
以點O為圓心，以3為半徑畫圓，交直線a和直線b分別有2個點，即有4個點符合；
③當MN=ON時，
作OM的垂直平分線分別交直線a，b于一點，即有2個點符合；
∴4+4+2=10，
故選D.
科目：初中數學 來源： 題型：
【題目】已知：在△ABC中，∠ACB=90°，點P是線段AC上一點，過點A作AB的垂線，交BP的延長線于點M，MN⊥AC于點N，PQ⊥AB于點Q，AQ=MN． 求證：
（1）△APM是等腰三角形；
（2）PC=AN．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB=AD，對角線AC，BD交于點E，點O在線段AE上，⊙O過B，D兩點，若OC=5，OB=3，且cos∠BOE=
．求證：CB是⊙O的切線．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在大同市開張的美化城市活動中，某居民小區要在一塊一邊靠墻（墻長
）的空地上修建一個矩形花園
，花園的一邊靠前，另三邊用總長為
的柵欄圍成（如圖所示），若設花園的
長為
，花園的面積為
．
求
與
之間的函數關系式，并寫出自變量的取值范圍；
滿足條件的花園面積能達到
嗎？若能，求出此時的值；若不能，說明理由；
根據中求得的函數關系式，描述其圖象的變化趨勢；并結合題意判斷當取何值時，花園的面積最大？最大面積為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩個文具店均出售鋼筆和筆記本，其中每支鋼筆定價10元，每本筆記本定價5元．兩個文具店在開展促銷活動中，各自提出優惠方案如下：
甲店：買一支鋼筆送一本筆記本；
乙店：買鋼筆或筆記本都按定價的80%付款.
現小明要購買鋼筆30支，筆記本
本(＞30)．
（1）試用含的代數式表示：
①小明到甲店購買所付款為 元；
②小明到乙店購買所付款為 元；
（2）當
40時，你能幫小明設計一種最為省錢的購買方案嗎？試寫出你的購買方案，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
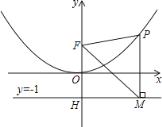
【題目】如圖所示，二次函數圖象的頂點在原點O，且經過點（1，
）.點F（0，1）在y軸上．直線y=－1與y軸交于點H．
（1）求該二次函數的解析式；
（2）設點P是（1）中圖象上在第一象限內的動點，過點P作x軸的垂線與直線y=－1交于點M.
①求證：FM平分∠OFP；
②當△FPM是等邊三角形時，試求P點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
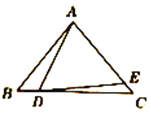
【題目】如圖所示，D、E分別是△ABC的邊BC、AC上的點，且AB=AC，AD=AE.
（1）若∠BAD=20°，則∠EDC= °.
（2）若∠EDC=20°，則∠BAD= °.
（3）設∠BAD=α，∠EDC=β，你能由（1）（2）中的結果找到α、β間所滿足的關系嗎?請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，AC=BC=AD．
（1）作∠A的平分線交CD于E；
（2）過B作CD的垂線，垂足為F；
（3）請寫出圖中兩對全等三角形（不添加任何字母），并選擇其中一對加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】要建一個如圖所示的面積為300
的長方形圍欄，圍欄總長50m，一邊靠墻（墻長25m），
（1）求圍欄的長和寬；
（2）能否圍成面積為400 的長方形圍欄？如果能，求出該長方形的長和寬，如果不能請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com