
如圖,已知二次函數的圖象經過點A(3,3)、B(4,0)和原點O.P為二次函數圖象上的一個動點,過點P作x軸的垂線,垂足為D(m,0),并與直線OA交于點C.
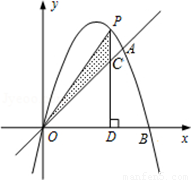
(1)求出二次函數的解析式;
(2)當點P在直線OA的上方時,用含m的代數式表示線段PC的長,并求線段PC的最大值;
(3)當m>0時,探索是否存在點P,使得△PCO為等腰三角形,如果存在,請直接寫出所有P的坐標;如果不存在,請說明理由.
(1)設y=ax(x﹣4),把A點坐標(3,3)代入得:a=﹣1,
函數的解析式為y=﹣x2+4x, …………………………………………………4分
(2)0<m<3,PC=PD﹣CD=﹣m2+3m,=﹣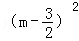 +
+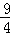 ,……………… 6分
,……………… 6分
∵﹣1<0,開口向下,∴有最大值,
當D(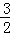 ,0)時,PCmax=
,0)時,PCmax=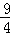 ,…………………………………………………8分
,…………………………………………………8分
(3)P的坐標是(3﹣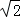 ,1+2
,1+2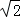 )或(3+
)或(3+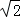 ,1﹣2
,1﹣2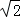 )或(5,﹣5)或(4,0).
)或(5,﹣5)或(4,0).
………………………………………………………………………12分
(3)簡單解答過程如下:
當0<m<3時,僅有OC=PC,∴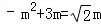 ,解得
,解得 ,
,
∴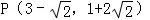 ;
;
當m≥3時,PC=CD﹣PD=m2﹣3m,OC= ,
,
由勾股定理得:OP2=OD2+DP2=m2+m2(m﹣4)2,
①當OC=PC時,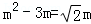 ,
,
解得: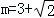 ,
,
∴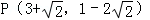 ;
;
②當OC=OP時,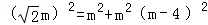 ,
,
解得:m1=5,m2=3(舍去),
∴P(5,﹣5);
③當PC=OP時,m2(m﹣3)2=m2+m2(m﹣4)2,
解得:m=4,
∴P(4,0),
存在P的坐標是(3﹣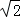 ,1+2
,1+2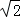 )或(3+
)或(3+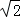 ,1﹣2
,1﹣2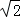 )或(5,﹣5)或(4,0).
)或(5,﹣5)或(4,0).
【解析】(1)設y=ax(x-4),把A點坐標代入即可求出答案;
(2)根據點的坐標求出PC=-m2+3m,化成頂點式即可求出線段PC的最大值;
(3)當0<m<3時,僅有OC=PC,列出方程,求出方程的解即可;當m≥3時,PC=CD-PD=m2-3m,OC= m,分為三種情況:①當OC=PC時,m2-3m=
m,分為三種情況:①當OC=PC時,m2-3m= m,求出方程的解即可得到P的坐標;同理可求:②當OC=OP時,③當PC=OP時,點P的坐標.綜合上述即可得到答案.
m,求出方程的解即可得到P的坐標;同理可求:②當OC=OP時,③當PC=OP時,點P的坐標.綜合上述即可得到答案.


 優等生題庫系列答案
優等生題庫系列答案 53天天練系列答案
53天天練系列答案科目:初中數學 來源: 題型:
 的一個動點,過點P作x軸的垂線,垂足為D(m,0),并與直線OA交于點C.
的一個動點,過點P作x軸的垂線,垂足為D(m,0),并與直線OA交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•呼和浩特)如圖,已知二次函數的圖象經過點A(6,0)、B(-2,0)和點C(0,-8).
(2013•呼和浩特)如圖,已知二次函數的圖象經過點A(6,0)、B(-2,0)和點C(0,-8).| 6 |
| 7 |
| 6 |
| 7 |
查看答案和解析>>
科目:初中數學 來源: 題型:
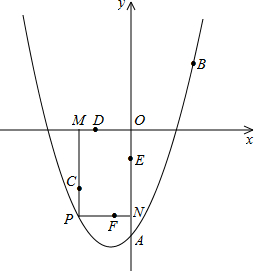 (2013•常德)如圖,已知二次函數的圖象過點A(0,-3),B(
(2013•常德)如圖,已知二次函數的圖象過點A(0,-3),B(| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知二次函數的圖象與x軸交于A(2,0)、B(6,0)兩點,與y軸交于點D(0,4).
如圖,已知二次函數的圖象與x軸交于A(2,0)、B(6,0)兩點,與y軸交于點D(0,4).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com