
【題目】(題文)(問題引領)
問題1:在四邊形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分別是AB,AD上的點.且∠ECF=60°.探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是,延長FD到點G.使DG=BE.連結CG,先證明
△CBE≌△CDG,再證明△CEF≌△CGF.他得出的正確結論是________________.

(探究思考)
問題2:若將問題1的條件改為:四邊形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 問題1的結論是否仍然成立?請說明理由.
∠BCD, 問題1的結論是否仍然成立?請說明理由.

(拓展延伸)
問題3:在問題2的條件下,若點E在AB的延長線上,點F在DA的延長線上,則問題2的結論是否仍然成立?若不成立,猜測此時線段BE、DF、EF之間存在什么樣的等量關系?并說明理由.

【答案】EF=BE+DF
【解析】
問題1,先證明△CBE≌△CDG,再證明△CEF≌△CGF,最后用線段的和差即可得出結論;
問題2、先判斷出∠ABC=∠GDC,進而判斷出△CBE≌△CDG,再證明△CEF≌△CGF,最后用線段的和差即可得出結論;
問題3、同問題2的方法即可得出結論.
問題1、BE+FD=EF,
理由:延長FD到點G.使DG=BE.連結CG,
在△CBE和△CDG中,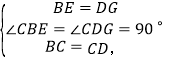
∴△CBE≌△CDG(SAS),
∴CE=CG,∠BCE=∠DCG,
∵![]()
∴![]()
∵![]()
∴∠ECF=∠GCF,
在△CEF和△CGF中,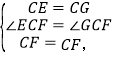
∴△CEF≌△CGF,
∴EF=GF,
∴EF=DF+DG=DF+BE;
故答案為:EF=DF+BE;
問題2,問題1中結論仍然成立,如圖2,
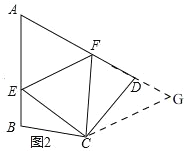
理由:延長FD到點G.使DG=BE.連結CG,
∵![]()
∴∠ABC=∠GDC,
在△CBE和△CDG中,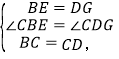
∴△CBE≌△CDG(SAS),
∴CE=CG,∠BCE=∠DCG,
∴∠BCD=∠ECG,
∵![]()
∴![]()
∴∠ECF=∠GCF,
在△CEF和△CGF中,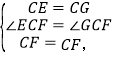
∴△CEF≌△CGF,
∴EF=GF,
∴EF=DF+DG=DF+BE;
問題3.結論:DF=EF+BE;理由:如圖3,
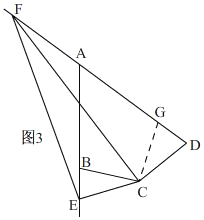
延長FD到點G.使DG=BE.連結CG,
∵![]()
∴∠ABC=∠GDC
在△CBE和△CDG中,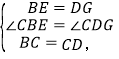
∴△CBE≌△CDG(SAS),
∴CE=CG,∠BCE=∠DCG,
∴∠BCD=∠ECG,
∵![]()
∴![]()
∴∠ECF=∠GCF,
在△CEF和△CGF中, 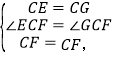
∴△CEF≌△CGF,
∴EF=GF,
∴DF=FG+DG=EF+BE;


科目:初中數學 來源: 題型:
【題目】如圖,某無人機于空中A處探測到目標B,D,從無人機A上看目標B,D的俯角分別為30°,60°,此時無人機的飛行高度AC為60m,隨后無人機從A處繼續飛行30 ![]() m到達A′處,
m到達A′處,
(1)求A,B之間的距離;
(2)求從無人機A′上看目標D的俯角的正切值. 
查看答案和解析>>
科目:初中數學 來源: 題型:
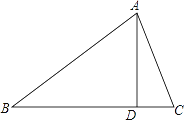
【題目】在△ABC中,∠B=40°,AD是BC邊上的高,且∠DAC=20°,則∠BAC=________.
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【題型】填空題
【結束】
16
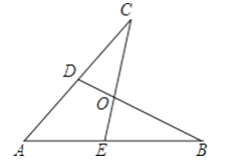
【題目】如圖所示,E,D是AB,AC上的兩點,BD,CE交于點O,且AB=AC,使△ACE≌△ABD,你補充的條件是________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=﹣ ![]() [(x﹣2)2+n]與x軸交于點A(m﹣2,0)和B(2m+3,0)(點A在點B的左側),與y軸交于點C,連結BC.
[(x﹣2)2+n]與x軸交于點A(m﹣2,0)和B(2m+3,0)(點A在點B的左側),與y軸交于點C,連結BC.
(1)求m、n的值;
(2)如圖2,點N為拋物線上的一動點,且位于直線BC上方,連接CN、BN.求△NBC面積的最大值;
(3)如圖3,點M、P分別為線段BC和線段OB上的動點,連接PM、PC,是否存在這樣的點P,使△PCM為等腰三角形,△PMB為直角三角形同時成立?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB的解析式為y=2x+5,與y軸交于點A,與x軸交于點B,點P為線段AB上的一個動點,作PE⊥y軸于點E,PF⊥x軸于點F,連接EF,則線段EF的最小值為 . 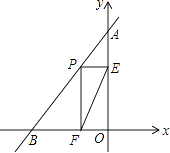
查看答案和解析>>
科目:初中數學 來源: 題型:
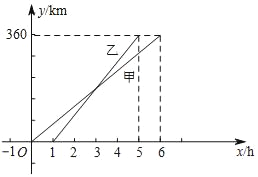
【題目】甲、乙兩人利用不同的交通工具,沿同一路線從A地出發前往B地,甲出發1h后,乙出發.設甲與A地相距y甲(km),乙與A地相距y乙(km),甲離開A地時間為x(h),y甲、y乙與x之間的函數圖象如圖所示.
(1)甲的速度是 km/h.
(2)請分別求出y甲、y乙與x之間的函數關系式.
(3)當乙與A地相距240km時,甲與B地相距多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E,F分別為邊AB,CD的中點,連接DE、BF、BD. 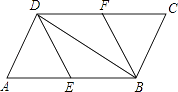
(1)求證:△ADE≌△CBF.
(2)若AD⊥BD,則四邊形BFDE是什么特殊四邊形?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是2002年北京第24屆國際數學家大會會徽,由4個全等的直角三角形拼合而成,如果大正方形的面積是13,小正方形的面積是1,直角三角形的短直角邊為a,較長直角邊為b,那么(a+b)2的值為( )
A.13
B.19
C.25
D.169
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com