
【題目】如圖,拋物線y=ax2+bx+c與x軸交于點A(﹣1,0),B(4,0),與y軸交于點C(0,2),點D與點C關于x軸對稱,點P是x軸上的一個動點,設點P的坐標為(m,0),過點P作x軸的垂線l,交拋物線于點Q.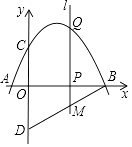
(1)求拋物線的解析式;
(2)求直線BD的解析式;
(3)當點P在線段OB上運動時,直線l交BD于點M,是否存在點P,使得四邊形CQMD是平行四邊形?若存在,求出m的值;若不存在,請說明理由.
【答案】
(1)
解:由題意可得 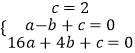 ,解得
,解得 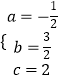 ,
,
∴拋物線解析式為y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:∵點C與點D關于x軸對稱,
∴D(0,﹣2),
∴可設直線BD解析式為y=kx﹣2,
把B(4,0)代入可得4k﹣2=0,解得k= ![]() ,
,
∴直線BD的解析式為y= ![]() x﹣2
x﹣2
(3)
解:如圖所示,
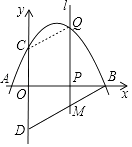
設Q(m,﹣ ![]() m2+
m2+ ![]() m+2),則M(m,
m+2),則M(m, ![]() m﹣2),
m﹣2),
∴QM=﹣ ![]() m2+
m2+ ![]() m+2﹣(
m+2﹣( ![]() m﹣2)=﹣
m﹣2)=﹣ ![]() m2+m+4,
m2+m+4,
∵QM∥CD,
∴當QM=CD時,四邊形CQMD是平行四邊形,
∴﹣ ![]() m2+m+4=4,解得m=0(不合題意,舍去)或m=2,
m2+m+4=4,解得m=0(不合題意,舍去)或m=2,
∴當m=2時,四邊形CQMD是平行四邊形
【解析】(1)由A、B、C的坐標,利用待定系數法可求得拋物線的解析式;(2)由對稱性可求得D點坐標,利用待定系數法可求得直線BD的解析式;(3)用m可表示出M、Q的坐標,則可表示出QM的長,由平行四邊形的性質可知QM∥CD且QM=CD,則可得到關于m的方程,可求得m的值.


科目:初中數學 來源: 題型:
【題目】如圖,學校環保社成員想測量斜坡 ![]() 旁一棵樹
旁一棵樹 ![]() 的高度,他們先在點
的高度,他們先在點 ![]() 處測得樹頂
處測得樹頂 ![]() 的仰角為
的仰角為 ![]() ,然后在坡頂
,然后在坡頂 ![]() 測得樹頂
測得樹頂 ![]() 的仰角為
的仰角為 ![]() ,已知斜坡
,已知斜坡 ![]() 的長度為
的長度為 ![]() ,
, ![]() 的長為
的長為 ![]() ,則樹
,則樹 ![]() 的高度是( )
的高度是( ) ![]()
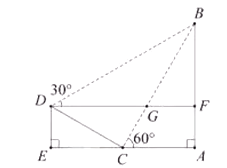
A.![]()
B.30
C.![]()
D.40
查看答案和解析>>
科目:初中數學 來源: 題型:
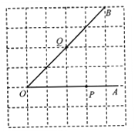
【題目】如圖,點P,Q分別是∠AOB的邊OA,OB上的點.
(1)過點P畫OB的垂線,垂足為H;
(2)過點Q畫OA的垂線,交OA于點C,連接PQ;
(3)線段QC的長度是點Q到 的距離, 的長度是點P到直線OB的距離,因為直線外一點和直線上各點連接的所有線段中,垂線段最短,所以線段PQ、PH的大小關系是 (用“<”號連接).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“世界那么大,我想去看看”一句話紅遍網絡,騎自行車旅行越來越受到人們的喜愛,各種品牌的山地自行車相繼投放市場.某車行經營的A型車2016年4月份銷售總額為3.2萬元,今年經過改造升級后A型車每輛銷售價比去年增加400元,若今年4月份與去年4月份賣出的A型車數量相同,則今年4月份A型車銷售總額將比去年4月份銷售總額增加25%.(A、B兩種型號車今年的進貨和銷售價格如下表所示)
A型車 | B型車 | |
進貨價格(元/輛) | 1100 | 1400 |
銷售價格(元/輛) | 今年的銷售價格 | 2400 |
(1)求今年4月份A型車每輛銷售價多少元(用列方程進行解答);
(2)該車行計劃5月份新進一批A型車和B型車共50輛,設購進的A型車為x輛,獲得的總利潤為y元,請寫出y與x之間的函數關系式;
(3)在(2)的條件下,若B型車的進貨數量不超過A型車數量的兩倍,應如何進貨才能使這批車獲利最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】十八世紀瑞士數學家歐拉證明了簡單多面體中頂點數(V)、面數(F)、棱數(E)之間存在的一個有趣的關系式,被稱為歐拉公式.請你觀察下列幾種簡單的多面體模型,解答下列問題:
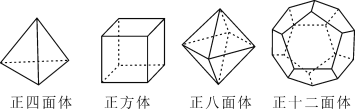
(1)根據上面的多面體模型,完成表格:
多面體 | 頂點數(V) | 面數(F) | 棱數(E) |
四面體 | 4 | 4 | |
正方體 | 8 | 12 | |
正八面體 | 6 | 8 | 12 |
正十二面體 | 20 | 12 | 30 |
可以發現頂點數(V)、面數(F)、棱數(E)之間存在的關系式是_______________;
(2)若一個多面體的面數比頂點數大8,且有30條棱,則這個多面體的面數是______;
(3)某個玻璃飾品的外形是簡單多面體,它的外表面是由三角形和八邊形兩種多邊形拼接而成,且有24個頂點,每個頂點處有3條棱.設該多面體外表面三角形的個數為x,八邊形的個數為y,求x+y的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,∠BAC=90°,點D是直線AB上的一動點(不和A、B重合),BE⊥CD于E,交直線AC于F.
(1)點D在邊AB上時,請證明:BD=AB﹣AF;
(2)試探索:點D在AB的延長線或反向延長線上時,請在備用圖中畫出圖形,(1)中的結論是否成立?若不成立,請直接寫出正確結論(不需要證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將正方形OABC放在平面直角坐標系中,O是原點,A的坐標為(1, ![]() ),則點B的坐標為( )
),則點B的坐標為( ) 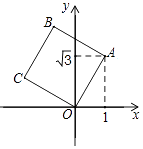
A.(1﹣ ![]() ,
, ![]() +1)
+1)
B.(﹣ ![]() ,
, ![]() +1)??
+1)??
C.(﹣1, ![]() +1)
+1)
D.(﹣1, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com