
如圖,直線y= x+m(m≠0)交x軸負半軸于點A、交y軸正半軸于點B且AB=5,過點A作直線AC⊥AB交y軸于點C.點E從坐標原點O出發,以0.8個單位/秒的速度沿y軸向上運動;與此同時直線l從與直線AC重合的位置出發,以1個單位/秒的速度沿射線AB方向平行移動.直線l在平移過程中交射線AB于點F、交y軸于點G.設點E離開坐標原點O的時間為t(t≥0)s.
x+m(m≠0)交x軸負半軸于點A、交y軸正半軸于點B且AB=5,過點A作直線AC⊥AB交y軸于點C.點E從坐標原點O出發,以0.8個單位/秒的速度沿y軸向上運動;與此同時直線l從與直線AC重合的位置出發,以1個單位/秒的速度沿射線AB方向平行移動.直線l在平移過程中交射線AB于點F、交y軸于點G.設點E離開坐標原點O的時間為t(t≥0)s.
(1)求直線AC的解析式;
(2)直線l在平移過程中,請直接寫出△BOF為等腰三角形時點F的坐標;
(3)直線l在平移過程中,設點E到直線l的距離為d,求d與t的函數關系.
(1)y=﹣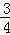 x﹣
x﹣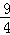 (2)F1(
(2)F1( ,
,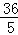 )、F2(﹣
)、F2(﹣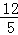 ,
, )、F3.(﹣
)、F3.(﹣ ,2)
,2)
(3)d=﹣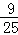 t+
t+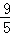 d=
d=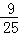 t﹣
t﹣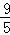
解析試題分析:(1)∵y=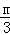 x+m交x軸負半軸于點A、交y軸正半軸于點B,
x+m交x軸負半軸于點A、交y軸正半軸于點B,
∴B(0,m)、A(﹣3,0).
∵AB=5,
∴m2+32=52,
解得m=±4.
∵m>0,
∴m=4.
∴B(0,4).
∴OB=4.
∵直線AC⊥AB交y軸于點C,易得△BOA∽△AOC,
∴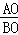 =
=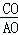 .
.
∴CO=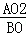 =
=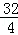 =
=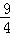 .
.
∵點C在y軸負半軸上,
∴C(0,﹣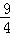 ).
).
設直線AC解析式為y=kx+b,
∵A(﹣3,0),C(0,﹣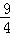 ),
),
∴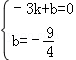 ,
,
解得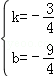 ,
,
∴y=﹣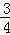 x﹣
x﹣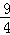 ;
;
(2)F1( ,
,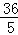 )、F2(﹣
)、F2(﹣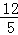 ,
, )、F3.(﹣
)、F3.(﹣ ,2);
,2);
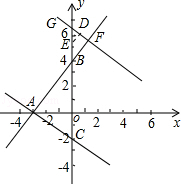
(3)分兩種情況:第一種情況:當0≤t≤5時,
如圖,作ED⊥FG于D,則ED=d.
由題意,FG∥AC,
∴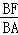 =
=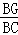 ,
,
∵AF=t,AB=5,
∴BF=5﹣t.
∵B(0,4),
∴BC=4+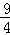 =
=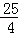 .
.
∴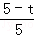 =
= .
.
∴BG= (5﹣t).
(5﹣t).
∵OE=0.8t,OB=4,
∴BE=4﹣0.8t.
∴EG= (5﹣t)﹣(4﹣0.8t)=
(5﹣t)﹣(4﹣0.8t)=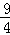 ﹣
﹣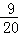 t.
t.
∵FG⊥AB,ED⊥FG,
∴∠GDE=∠GFB=90°.
∴ED∥AB.
∴ =
= .
.
∴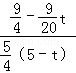 =
=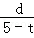 .
.
∴d=﹣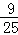 t+
t+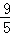 .
.
第二種情況:當t>5時,
如圖(2),
作ED⊥FG于D,則ED=d,
則題意,FG∥AC,
∴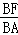 =
=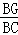 .
.
∵AF=t,AB=5,
∴BF=t﹣5.
∵B(0,4),C(0,﹣ ),
),
∴BC=4+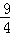 =
= .
.
∴ =
= .
.
∴BG=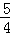 (t﹣5).
(t﹣5).
∵OE=0.8t,OB=4,
∴BE=0.8t﹣4,EG=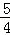 (t﹣5)﹣(0.8t﹣4),
(t﹣5)﹣(0.8t﹣4),
=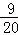 t﹣
t﹣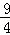 .
.
∵FG⊥AB,ED⊥FG,∠GDE=∠GFB=90°,
∴ED∥AB.
∴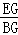 =
=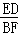 .
.
∴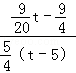 =
=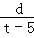 .
.
∴d=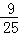 t﹣
t﹣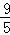 .
.
考點:一次函數綜合題;待定系數法求一次函數解析式;兩條直線相交或平行問題;等腰三角形的性質;相似三角形的判定與性質.
點評:此題考查了一次函數的綜合;解題的關鍵是求出各點的坐標,再用各點的坐標求出解析式,注意(3)中分兩種情況進行討論,不要漏掉.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 13、如圖,直線a、b都與直線c相交,給出下列條件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判斷a∥b的是( )
13、如圖,直線a、b都與直線c相交,給出下列條件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判斷a∥b的是( )查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,直線y=6-x交x軸、y軸于A、B兩點,P是反比例函數y=
如圖,直線y=6-x交x軸、y軸于A、B兩點,P是反比例函數y=| 4 |
| x |
| A、8 | ||
| B、6 | ||
| C、4 | ||
D、6
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com