
【題目】如圖,在平面直角坐標系內,已知直線l1經過原點O 及A(2,2 ![]() )兩點,將直線l1向右平移4個單位后得到直線l2 , 直線l2與x 軸交于點B.
)兩點,將直線l1向右平移4個單位后得到直線l2 , 直線l2與x 軸交于點B. 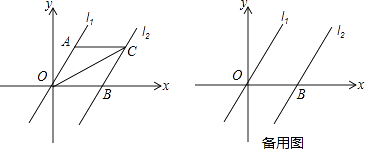
(1)求直線l2的函數表達式;
(2)作∠AOB 的平分線交直線l2于點C,連接AC.求證:四邊形OACB是菱形;
(3)設點P 是直線l2上一點,以P 為圓心,PB 為半徑作⊙P,當⊙P 與直線l1相切時,請求出圓心P 點的坐標.
【答案】
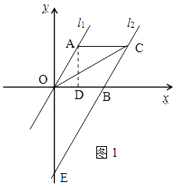
(1)解:過點A作AD⊥x軸于點D,設直線l2與y軸交于點E,(如圖1)
∵A(2, ![]() ),
),
∴AD= ![]() ,OD=2,
,OD=2,
∵l2∥l1,
∴∠OBE=∠AOD,
∴tan∠OBE=tan∠AOD= ![]() ,
,
∵OB=4,
∴OE= ![]() OB=
OB= ![]() ,
,
∴B(4,0)、E(0, ![]() ),
),
設直線l2為y=kx+b,則 ![]() ,
,
解得: ![]() ,
,
∴直線l2的函數表達式為 ![]() .
.
(2)證明:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵l2∥l1,
∴∠AOC=∠BCO,
∴∠BOC=∠BCO,
∴BC=OB=4,
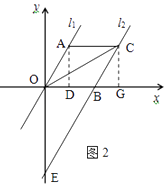
過點C作CG⊥x軸于點G,(如圖2)
∵∠CBG=∠AOD=60°,
∴CG= ![]() ,BG=
,BG= ![]() ,
,
∴OG=OB+BG=4+2=6,
∴C(6, ![]() ),
),
∵A(2, ![]() ),
),
∴AC∥OB,
∵BC∥OA,
∴四邊形OACB是平行四邊形,
∵OB=BC,
∴四邊形OACB是菱形.
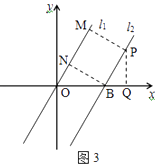
(3)解:當點P在x軸上方時,
過點P作PM⊥l1于點M,過點B作BN⊥l1于點N,過點PQ⊥x軸于點Q,(如圖3)
則 PB=PM=BN=OBsin∠BOM=4sin60°= ![]() ,
,
∴PQ=PBsin∠PBQ= ![]() sin60°=3,
sin60°=3,
BQ=PBcos∠PBQ= ![]() cos60°=
cos60°= ![]() ,
,
∴OQ=OB+BQ=4+ ![]() ,
,
∴P(4+ ![]() ,3),
,3),
當點P在x軸下方時,同理可得P(4﹣ ![]() ,﹣3),
,﹣3),
∴點P的坐標為(4+ ![]() ,3)或P(4﹣
,3)或P(4﹣ ![]() ,﹣3)
,﹣3)
【解析】(1)過點A作AD⊥x軸于點D,設直線l2與y軸交于點E,由A的坐標可知AD與OD的長度,進而求出E的坐標,利用待定系數法即可求出直線l2的解析式.(2)由角平分線的性質可知:∠AOC=∠BOC,過點C作CG⊥x軸于點G,由于l2∥l1 , 所以∠AOC=∠BCO,從而可知:∠BOC=∠BCO,過點C作CG⊥x軸于點G,求出A、C的坐標可知兩點的縱坐標相等,從而可知AC∥OB,由于OB=OC,所以四邊形OACB是菱形;(3)由于點P的位置不確定,故需要分兩種情況討論,一是點P在x軸上方,二是點P在x軸下方,然后根據切線的性質即可求出P的坐標.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
【題目】問題探究:如圖①,四邊形 ABCD是正方形,BE⊥BF,BE=BF,求證:△ABE≌△CBF;
方法拓展:如圖②,ABCD是矩形,BC=2AB,BF⊥BE,BF=2BE,若矩形ABCD的面積為40,△ABE的面積為4,求陰影部分圖形的面積.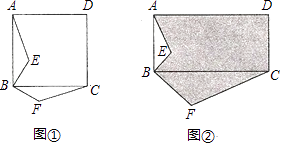
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,將△ABO繞點A順時針旋轉到△AB1C1的位置,點B、O分別落在點B1、C1處,點B1在x軸上,再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置,點C2在x軸上,將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置,點A2在x軸上,依次進行下去….若點A(3,0),B(0,4),則點B100的坐標為 . 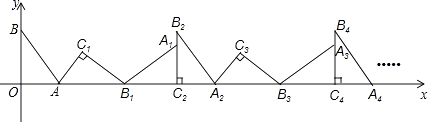
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,過點B(6,0)的直線AB與直線OA相交于點A(4,2),動點M在y軸上運動.
(1)求直線AB的函數解析式;
(2)動點M在y軸上運動,使MA+MB的值最小,求點M的坐標;
(3)在y軸的負半軸上是否存在點M,使△ABM是以AB為直角邊的直角三角形?如果存在,求出點M的坐標;如果不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]()
(Ⅰ)求證:方程有兩個不相等的實數根;
(Ⅱ)若此方程的一個根是1,請求出方程的另一個根;
(Ⅲ)求以(Ⅱ)中所得兩根為邊長的等腰三角形的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是( )
,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是( ) 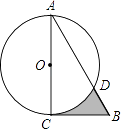
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com