
(10分)如圖,已知拋物線與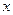 軸交于A(1,0),B(
軸交于A(1,0),B(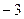 ,0)兩點,與
,0)兩點,與 軸交于點
軸交于點
C(0,3),拋物線的頂點為P,連結AC.
(1)求此拋物線的解析式;
(2)在拋物線上找一點D,使得DC與AC垂直,且直線DC與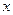 軸交于點Q,求點D的坐標;
軸交于點Q,求點D的坐標;
(3)拋物線對稱軸上是否存在一點M,使得S△MAP=2S△ACP,若存在,求出M點坐標;若不存在,請說明理由.
(10分)解(1)設此拋物線的解析式為:

∵拋物線與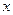 軸交于A(1,0)、B(
軸交于A(1,0)、B( 兩點,
兩點,
∴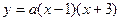
又∵拋物線與 軸交于點C(0,3)
軸交于點C(0,3)
∴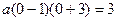 ,
,
∴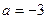
 ∴
∴
即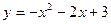 ……………3分
……………3分
用其他解法參照給分
(2)∵點A(1,0),點C(0,3)
∴OA=1,OC=3,
∵DC⊥AC,OC⊥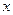 軸
軸
∴△QOC∽△COA
∴ ,即
,即
∴OQ=9,……………………4分
又∵點Q在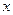 軸的負半軸上,∴Q(
軸的負半軸上,∴Q(
設直線DC的解析式為: ,則
,則 解之得:
解之得:
∴直線DC的解析式為: ……………………5分
……………………5分
∵點D是拋物線與直線DC的交點,
∴ 解之得:
解之得: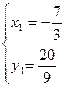
 (不合題意,應舍去)
(不合題意,應舍去)
∴點D( ……………………6分
……………………6分
用其他解法參照給分
(3)如圖,點M為直線 上一點,連結AM,PC,PA
上一點,連結AM,PC,PA
設點M( ,直線
,直線 與
與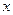 軸交于點E,∴AE=2
軸交于點E,∴AE=2
∵拋物線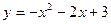 的頂點為P,對稱軸為
的頂點為P,對稱軸為
∴P(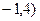
∴PE=4
則PM=
∵S四邊形AEPC=S四邊形OEPC+S△AOC
=
=
=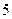 ……………………7分
……………………7分
又∵S四邊形AEPC= S△AEP+S△ACP
S△AEP=
∴+S△ACP= ……………………8分
……………………8分
∵S△MAP=2S△ACP
∴
∴
∴ ,
,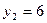 ……………………9分
……………………9分
故拋物線的對稱軸上存在點M使S△MAP=2S△ACP
點M( 或
或 ……………………10分
……………………10分
用其他解法參照給分
解析


科目:初中數(shù)學 來源: 題型:
(本題滿分10分)如圖,已知![]() ,以
,以![]() 為直徑,
為直徑,![]() 為圓心的半圓交
為圓心的半圓交![]() 于點
于點![]() ,點
,點![]() 為弧CF的中點,連接
為弧CF的中點,連接![]() 交
交![]() 于點
于點![]() ,
,![]() 為△ABC的角平分線,且
為△ABC的角平分線,且![]() ,垂足為點
,垂足為點![]() .
.
(1)求證:![]() 是半圓
是半圓![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
(本題滿分10分)
如圖,已知OA⊥OB,OA=8,OB=6,以AB為邊作矩形ABCD,使AD=a,過點D作DE垂直O(jiān)A的延長線交于點E.
(1)求證:△OAB∽△EDA;
(2)當a為何值時,△OAB與△EDA全等?并求出此時點C到OE的距離.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學 來源:2012屆浙江省杭州市九年級第一次中考模擬考試數(shù)學卷 題型:選擇題
(本題滿分10分)如圖,已知 ,以
,以 為直徑,
為直徑, 為圓心的半圓交
為圓心的半圓交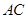 于點
于點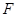 ,點
,點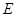 為弧CF的中點,連接
為弧CF的中點,連接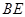 交
交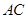 于點
于點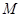 ,
,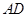 為△ABC的角平分線,且
為△ABC的角平分線,且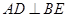 ,垂足為點
,垂足為點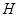 . [來源:]
. [來源:]
(1)求證: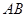 是半圓
是半圓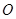 的切線;
的切線;
(2)若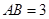 ,
,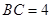 ,求
,求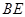 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源:2011年初中畢業(yè)升學考試(山東聊城卷)數(shù)學 題型:解答題
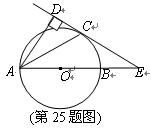
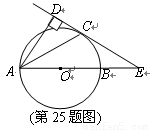
(11·柳州)(本題滿分10分)
如圖,已知AB是⊙O的直徑,銳角∠DAB的平分線AC交⊙O于點C,作CD⊥AD,垂足為D,直線CD與AB的延長線交于點E.
(1)求證:直線CD為⊙O的切線;
(2)當AB=2BE,且CE=時,求AD的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com