【題目】如圖，在平面內直角坐標系中，直線l：y= 
x+1交x軸于點A，交y軸于點B，點A1 ， A2 ， A3 ， …在x軸上，點B1、B2、B3 ， …在直線l上．若△OB1A1 ， △A1B2A2 ， △A2B3A3 ， …均為等邊三角形，則OAn的長是（ ）
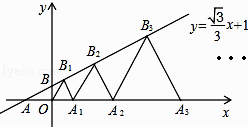
A.2n 
B.（2n+1）
C.（2n﹣1﹣1）
D.（2n﹣1）
舉一反三單元同步過關卷系列答案科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，AB=AC，點D為BC中點，AN是△ABC外角∠CAM的平分線，CE⊥AN，垂足為點E．求證：四邊形ADCE為矩形．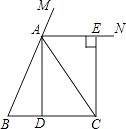 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖（1）所示，∠AOB、∠COD都是直角．
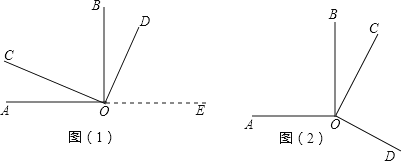
（1）試猜想∠AOD與∠COB在數量上是相等，互余，還是互補的關系．請你用推理的方法說明你的猜想是合理的．
（2）當∠COD繞著點O旋轉到圖（2）所示位置時，你在（1）中的猜想還成立嗎？請你證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知拋物線y=ax2+bx﹣2（a≠0）與x軸交于A（1，0）、B（3，0）兩點，與y軸交于點C，其頂點為D．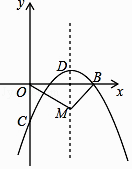 
（1）求拋物線的解析式；
（2）一動點M從點D出發，以每秒1個單位的速度沿拋物線的對稱軸向下運動，連OM，BM，設運動時間為t秒（t=0），在點M的運動過程中，當∠OMB=90°時，求t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y=ax2+bx+c的圖像如圖所示，則下列結論：
①abc＞0；②a+b+c=2；③b＞1；④a＜ 
．
其中正確的結論是（ ）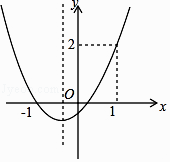
A.①②
B.②③
C.③④
D.②④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知四邊形ABCD是矩形，cot∠ADB= 
，AB=16．點E在射線BC上，點F在線段BD上，且∠DEF=∠ADB．
（1）求線段BD的長；
（2）設BE=x，△DEF的面積為y，求y關于x的函數關系式，并寫出函數定義域；
（3）當△DEF為等腰三角形時，求線段BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，連接BD，點O是BD的中點，若M、N是邊AD上的兩點，連接MO、NO，并分別延長交邊BC于兩點M′、N′，則圖中的全等三角形共有（ ）
A. 2對 B. 3對 C. 4對 D. 5對
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（教材回顧）課本88頁，有這樣一段文字：人們通過長期觀察發現如果早晨天空中棉絮的高積云，那么午后常有雷雨降臨，于是有了“朝有破絮云，午后雷雨臨”的諺語．在數學的學習過程中，我們經常用這樣的方法探究規律．
（數學問題）三角形有3個頂點，如果在它的內部再畫n個點，并以這(n+3)個點為頂點畫三角形，那么最多可以剪得多少個這樣的三角形？
（問題探究）為了解決這個問題，我們可以從n=1，n=2，n=3等具體的、簡單的情形入手，探索最多可以剪得的三角形個數的變化規律．
三角形內點的個數 | 圖形 | 最多剪出的小三角形個數 |
1 |
| 3 |
2 |
| 5 |
3 |
| 7 |
… | … | … |
（問題解決）
(1) 當三角形內有4個點時，最多剪得的三角形個數為______________；
(2) 你發現的變化規律是：三角形內的點每增加1個，最多剪得的三角形增加______個；
(3) 猜想：當三角形內點的個數為n時，最多可以剪得_______________個三角形；
像這樣通過對簡單情形的觀察、分析，從特殊到一般地探索這類現象的規律、提出猜想的思想方法稱為歸納．
（問題拓展）
（4）請你嘗試用歸納的方法探索1+3+5+7+…+（2n-1）+（2n+1）的和是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
