
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上一動點(不與點
邊上一動點(不與點![]() 重合),過點
重合),過點![]() 作
作![]() 交
交![]() 邊于點
邊于點![]() ,將
,將![]() 沿直線
沿直線![]() 翻折,點
翻折,點![]() 落在射線
落在射線![]() 上的點
上的點![]() 處,當
處,當![]() 為直角三角形時,求
為直角三角形時,求![]() 的長.
的長.
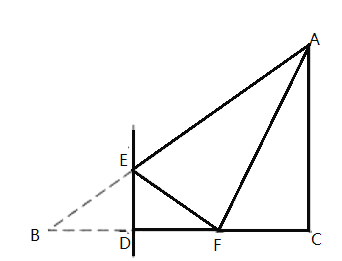
【答案】1或2
【解析】
由題意根據翻折的性質以及勾股定理和特殊銳角三角函數值進行綜合分析求解.
解:∵Rt△ABC中,∠ACB=90°,∠B=30°,
∴![]() ,
,
∵∠B=30°,DE⊥BC,
∴∠BED=60°,
由翻折的性質可知:∠BED=∠FED=60°,
∴∠AEF=60°,
∵△AEF為直角三角形,
∴∠EAF=30°,
∴AE=2EF,
由翻折的性質可知:BE=EF,
∴AB=3BE,
∴![]() ,
,
當點F在BC的延長線上時.
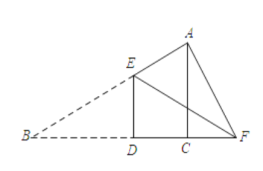
∵△AEF為直角三角形,
∴∠EAF=90°,
∴∠EFA=30°,
∴∠EFD=∠EFA,
又∵ED⊥BF,EA⊥AF,
∴AE=DE,
∵BC=3,∠ACB=90°,∠B=30°,
∴![]() ,
,
設![]() ,
,
∵DE∥AC,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴BD的長為1或2時,△AEF為直角三角形.


科目:初中數學 來源: 題型:
【題目】如圖,已知:關于x的二次函數![]() 的圖象與x軸交于點A(1,0)和點B,與y軸交于點C(0,3),拋物線的對稱軸與x軸交于點D.
的圖象與x軸交于點A(1,0)和點B,與y軸交于點C(0,3),拋物線的對稱軸與x軸交于點D.
(1)求二次函數的表達式;
(2)在y軸上是否存在一點P,使△PBC為等腰三角形.若存在,請求出點P的坐標;
(3)有一個點M從點A出發,以每秒1個單位的速度在AB上向點B運動,另一個點N從點D與點M同時出發,以每秒2個單位的速度在拋物線的對稱軸上運動,當點M到 達點B時,點M、N同時停止運動,問點M、N運動到何處時,△MNB面積最大,試求出最大面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
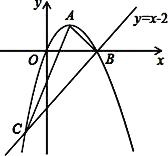
【題目】如圖,已知拋物線經過原點O,頂點為A(1,1),且與直線y=x﹣2交于B,C兩點.
⑴求拋物線的解析式及點C的坐標;
⑵求證:△ABC是直角三角形;
⑶若點N為x軸上的一個動點,過點N作MN⊥x軸與拋物線交于點M,則是否存在以O,M,N為頂點的三角形與△ABC相似?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,將坐標原點O沿x軸向左平移2個單位長度得到點A,過點A作y軸的平行線交反比例函數y=![]() 的圖象于點B,AB=
的圖象于點B,AB=![]() .
.
(1)求反比例函數的解析式;
(2)若P(x1,y1)、Q(x2,y2)是該反比例函數圖象上的兩點,且x1<x2時,y1>y2,指出點P、Q各位于哪個象限?并簡要說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知ABCD是一個以AD為直徑的圓內接四邊形,分別延長AB和DC,它們相交于P,若∠APD=60°,AB=5,PC=4,則⊙O的面積為( )
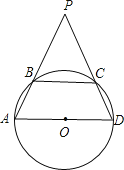
A. 25π B. 16π C. 15π D. 13π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線MN∥PQ,直線AB分別與MN,PQ相交于點A,B.小宇同學利用尺規按以下步驟作圖:①以點A為圓心,以任意長為半徑作弧交AN于點C,交AB于點D;②分別以C,D為圓心,以大于![]() CD長為半徑作弧,兩弧在∠NAB內交于點E;③作射線AE交PQ于點F.若AB=2,∠ABP=60°,則線段AF的長為_____.
CD長為半徑作弧,兩弧在∠NAB內交于點E;③作射線AE交PQ于點F.若AB=2,∠ABP=60°,則線段AF的長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+3交x軸于A點,將一塊等腰直角三角形紙板的直角頂點置于原點O,另兩個頂點M、N恰落在直線y=
x+3交x軸于A點,將一塊等腰直角三角形紙板的直角頂點置于原點O,另兩個頂點M、N恰落在直線y=![]() x+3上,若N點在第二象限內,則tan∠AON的值為( )
x+3上,若N點在第二象限內,則tan∠AON的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com