
【題目】如圖,已知BE和CF是△ABC的兩條高,∠ABC=48°,∠ACB=76°,則∠FDE= . 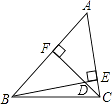
【答案】124°
【解析】解:(法一)在△ABC中, ∵∠A+∠ABC+∠ACB=180°
∴∠A=180°﹣48°﹣76°=56°
在四邊形AFDE中,
∵∠A+∠AFC+∠AEB+∠FDE=360°
又∵∠AFC=∠AEB=90°,∠A=56°
∴∠FDE=360°﹣90°﹣90°﹣56°
=124°
故答案為:124°
(法二)∵∠AEB=∠ACB+∠EBC=90°,∠AFC=∠ABC+∠FCB=90°,
∴∠CBE=14°,∠FCB=42°,
∵∠BDC=180°﹣∠CBE﹣∠FCB=124°,
∴∠FDE=124°.
故答案為:124°
由三角形的內角和定理求出∠A的度數,再有四邊形AFDE的內角和求出∠FDE的度數.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
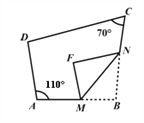
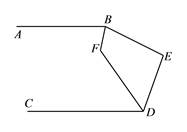
【題目】如圖,四邊形ABCD中,點M、N分別在AB、BC上,將BMN沿MN翻折,得FMN,若MF∥AD,FN∥DC,則∠D的度數為_________
查看答案和解析>>
科目:初中數學 來源: 題型:
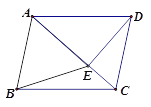
【題目】如圖,在四邊形ABCD中,AB//CD,∠ABC=∠ADC,DE垂直于對角線AC,垂足是E,連接BE .
(1)求證:四邊形ABCD是平行四邊形;
(2)若點E是AC的中點,判斷BE與AC的位置關系,并說明理由;
(3)若△ABE是等邊三角形,AD=![]() ,求對角線AC的長 .
,求對角線AC的長 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MON=30°,點A1 , A2 , A3 , …在射線ON上,點B1 , B2 , B3 , …在射線OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均為等邊三角形.若OA1=1,則△AnBnAn+1的邊長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
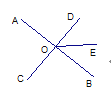
【題目】如圖3,直線AB、CD相交于O,若∠AOD比∠AOC大40°,則∠BOD=___°;若∠AOD=2∠AOC,則∠BOC=___;若∠AOD=∠AOC,則∠BOD=___.
查看答案和解析>>
科目:初中數學 來源: 題型:
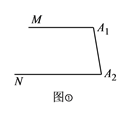
【題目】(1)如圖①,![]() ,則
,則![]() _________.
_________.
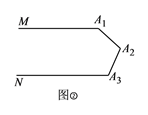
如圖②,![]() ,則
,則![]() ___________.
___________.
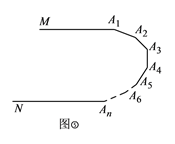
如圖③,![]() ,則
,則![]() ___________.
___________.
如圖④,![]() ,則
,則![]() ___________.
___________.
從上述結論中你發現了什么規律?請在圖②,圖③,圖④中選一個證明你的結論.


(2)如圖⑤,![]() ,則
,則![]() ______________.
______________.
(3)利用上述結論解決問題:如圖已知![]() ,
, ![]() 和
和![]() 的平分線相交于
的平分線相交于![]() ,
, ![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com