
【題目】已知拋物線y=ax2﹣2x+c的對稱軸為直線x=﹣1,頂點為A,與y軸正半軸交點為B,且△ABO的面積為1.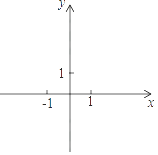
(1)求拋物線的表達式;
(2)若點P在x軸上,且PA=PB,求點P的坐標.
【答案】
(1)解:∵對稱軸為直線x=﹣1,
∴﹣ ![]() =﹣1,
=﹣1,
∴a=﹣1,
∵△ABO的面積為1,
∴ ![]() c×1=1,
c×1=1,
∴c=2,
∴拋物線的表達式為y=﹣x2﹣2x+2
(2)解:∵y=﹣x2﹣2x+2=﹣(x+1)2+3,
∴A(﹣1,3),
設P點的坐標為(x,0).
∵PA=PB,B(0,2),
∴(x+1)2+32=x2+22 ,
解得x=﹣3.
故P點的坐標為(﹣3,0)
【解析】(1)根據拋物線的對稱軸為x=-1求出a的值,再根據△AB0的面積為1,求出c的值,即可得出函數解析式。
(2)先求出頂點A的坐標,抓住點P在x軸上,且PA=PB,因此設P點的坐標為(x,0),利用勾股定理,根據PA=PB,建立方程求解即可得出點P的坐標。


科目:初中數學 來源: 題型:
【題目】一列快車從甲地駛往乙地,一列慢車從乙地駛往甲地,兩車同時出發,勻速行駛,設慢車行駛的時間x(h),兩車之間的距離為y(km),圖中的折線表示y與x之間的函數關系.根據圖象回答:
(1)甲、乙兩地之間的距離為 ;
(2)兩車同時出發后 h相遇;
(3)慢車的速度為 千米/小時;快車的速度為 千米/小時;
(4)線段CD表示的實際意義是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
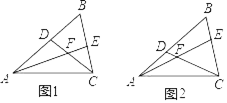
【題目】在△ABC中,∠B=60°,D、E分別為AB、BC上的點,且AE、CD交于點F.
(1)如圖1,若AE、CD為△ABC的角平分線:
①求∠AFD的度數;
②若AD=3,CE=2,求AC的長;
(2)如圖2,若∠EAC=∠DCA=30°,求證:AD=CE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《如果想毀掉一個孩子,就給他一部手機!》這是微信朋友圈熱傳的一篇文章.國際上,法國教育部宣布從2018年9月新學期起,小學和初中禁止學生使用手機.為了解學生手機使用情況,某學校開展了“手機伴我健康行”主題活動,他們隨機抽取部分學生進行“使用手機目的”和“每周使用手機的時間”的問卷調查,并繪制成如圖所示的統計圖,已知“查資料”的人數是![]() 人.
人.

請你根據以上信息解答下列問題:
![]() 求出本次隨機抽取的學生共有多少人;
求出本次隨機抽取的學生共有多少人;
![]() 在扇形統計圖中,“玩游戲”對應的百分比為______________,圓心角度數是_______________度;
在扇形統計圖中,“玩游戲”對應的百分比為______________,圓心角度數是_______________度;
![]() 補全條形統計圖;
補全條形統計圖;
![]() 該校共有學生
該校共有學生![]() 人,估計每周使用手機時間在
人,估計每周使用手機時間在![]() 小時以上(不含
小時以上(不含![]() 小時)的人數.
小時)的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課題小組從某市20000名九年級男生中,隨機抽取了1000名進行50米跑測試,并根據測試結果制成了如下的統計表.
等級 | 人數/名 | 百分比 |
優秀 | 200 | 20% |
良好 | 600 | 60% |
及格 | 150 | 15% |
不及格 | 50 | a |
(1)a的值為__________;
(2)請你從表格中任意選取一列數據,繪制合理的統計圖來表示;(繪制一種即可)

(3)說一說你選擇此統計圖的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知,![]() 滿足
滿足![]() 點在
點在![]() 軸的負半軸上,直角頂點
軸的負半軸上,直角頂點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上方.
軸上方.
![]() 如圖1所示,若點
如圖1所示,若點![]() 與原點重合,點
與原點重合,點![]() 的坐標是
的坐標是![]() ,則點
,則點![]() 的坐標是 ;
的坐標是 ;

![]() 如圖2所示,若點
如圖2所示,若點![]() 的坐標是
的坐標是![]() ,過點
,過點![]() 作
作![]() 軸于
軸于![]() ,請求出點
,請求出點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條不完整的數軸上從左到右有點A,B,C,其中AB=2,BC=1,如圖所示,設點A,B,C所對應數的和是p. ![]()
(1)若以B為原點,寫出點A,C所對應的數,并計算p的值;若以C為原點,p又是多少?
(2)若原點O在圖中數軸上點C的右邊,且CO=28,求p.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強學生課外閱讀,開闊視野,某校開展了“書香校園,從我做起”的主題活動.學校隨機抽取了部分學生,對他們一周的課外閱讀時間進行調查,繪制出頻數分布表和頻數分布直方圖的一部分如下:
課外閱讀時間(單位:小時) | 頻數(人數) | 頻率 |
0﹤t≤2 | 2 | 0.04 |
2﹤t≤4 | 3 | 0.06 |
4﹤t≤6 | 15 | 0.30 |
6﹤t≤8 | a | 0.50 |
t﹥8 | 5 | b |

請根據圖表信息回答下列問題:
(1)頻數分布表中的a=b=;
(2)將頻數分布直方圖補充完整;
(3)學校將每周課外閱讀時間在8小時以上的學生評為“閱讀之星”,請你估計該校2000名學生中評為“閱讀之星”的有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com