
【題目】如圖,在![]() 中,
中,![]() ,將
,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() ,得到
,得到![]() ,其中點
,其中點![]() 的對應點分別為點
的對應點分別為點![]() 連接
連接![]() 在旋轉過程中,若
在旋轉過程中,若![]() ,則
,則![]() 的長為_________.
的長為_________.

【答案】![]()
【解析】
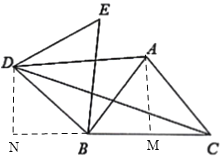
如圖,過點A作AM⊥BC于M,過點D作DN⊥BC,交CB延長線于N,根據旋轉的性質可得∠EBC=∠DBA,BD=AB,可得BD=AC,由![]() 可得∠DBA=∠BAC,即可證明BD//AC,可證明四邊形DBCA是平行四邊形,可得AM=DN,根據等腰三角形“三線合一”的性質可得BM=
可得∠DBA=∠BAC,即可證明BD//AC,可證明四邊形DBCA是平行四邊形,可得AM=DN,根據等腰三角形“三線合一”的性質可得BM=![]() BC,利用勾股定理可求出AM的長,可得DN的長,利用勾股定理可求出BN的長,進而可得CN的長,利用勾股定理求出CD的長即可.
BC,利用勾股定理可求出AM的長,可得DN的長,利用勾股定理可求出BN的長,進而可得CN的長,利用勾股定理求出CD的長即可.
如圖,過點A作AM⊥BC于M,過點D作DN⊥BC,交CB延長線于N,
∵AB=AC=5,BC=6,AM⊥BC,
∴BM=![]() BC=3,
BC=3,
∴AM=![]() =4,
=4,
∵將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() ,得到
,得到![]() ,
,
∴∠EBC=∠DBA,BD=AB=AC=5,
∵![]() ,
,
∴∠DBA=∠BAC,
∴BD//AC,
∴四邊形DBCA是平行四邊形,
∴DN=AM=4,
∴BN=![]() =3,
=3,
∴CN=BC+BN=9,
∴CD=![]() =
=![]() ,
,
故答案為:![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
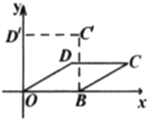
【題目】我們知道:四邊形具有不穩定性.如圖,在平面直角坐標系中,將邊長為4的菱形![]() 的邊
的邊![]() 固定在
固定在![]() 軸上,開始時
軸上,開始時![]() ,現把菱形向左推,使點
,現把菱形向左推,使點![]() 落在
落在![]() 軸正半軸上的點
軸正半軸上的點![]() 處,則下列說法中錯誤的是( )
處,則下列說法中錯誤的是( )
A.點![]() 的坐標為
的坐標為![]() B.
B.![]()
C.點![]() 移動的路徑長度為4個單位長度D.
移動的路徑長度為4個單位長度D.![]() 垂直平分
垂直平分![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與直線
與直線![]() 交于點
交于點![]() ,且點
,且點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)請用![]() 的代數式表示
的代數式表示![]() ;
;
(2)點![]() 在直線
在直線![]() 上,點
上,點![]() 的橫坐標為
的橫坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
①若拋物線![]() 過點
過點![]() ,求該拋物線的解析式;
,求該拋物線的解析式;
②若拋物線![]() 與線段
與線段![]() 恰有一個交點,直接寫出
恰有一個交點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線![]() (
(![]() ).
).
(1)寫出拋物線頂點的縱坐標 (用含a的代數式表示);
(2)若該拋物線與x軸的兩個交點分別為點A和點B,且點A在點B的左側,AB=4.
①求a的值;
②記二次函數圖象在點A,B之間的部分為W(含點A和點B),若直線![]() (
(![]() )經過(1,-1),且與圖形W有公共點,結合函數圖象,求b的取值范圍.
)經過(1,-1),且與圖形W有公共點,結合函數圖象,求b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 上一動點,以
上一動點,以![]() 為邊,在
為邊,在![]() 的右側作等邊
的右側作等邊![]() .
.
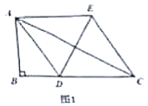

(1)當![]() 平分
平分![]() 時,如圖1,四邊形
時,如圖1,四邊形![]() 是________形;
是________形;
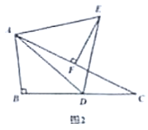
(2)過![]() 作
作![]() 于
于![]() ,如圖2,求證:
,如圖2,求證:![]() 為
為![]() 的中點;
的中點;
(3)若![]() .
.
①當![]() 為
為![]() 的中點時,過點
的中點時,過點![]() 作
作![]() 于
于![]() ,如圖3,求
,如圖3,求![]() 的長;
的長;
②點![]() 從
從![]() 點運動到
點運動到![]() 點,則點
點,則點![]() 所經過路徑長為________(直接寫出結果).
所經過路徑長為________(直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】作為國家級開發區的兩江新區,大小公園星羅棋布,稱為“百園之城”.該區2018年綠地總面積為2500萬平方米,2020年綠地總面積將比2018年增加3500萬平方米,人口比2018年增加50萬人.這樣,2020年該區人均綠地面積是2018年人均綠地面積的2倍.
(1)求2020年兩江新區的人口數量;
(2)2020年起,為了更好地建設“一半山水一半城”的美麗新區,吸引外來人才落戶兩江新區,新區管委會在增加綠地面積的同時大力擴展配套水域面積.根據調查,2020年新區的配套水域面積為人均4平方米.在2020年的基礎上,如果人均綠地每增加1平方米,人均配套水域將增加![]() 平方米,人口也將隨之增加5萬.這樣,兩江新區2022年的綠地總面積與配套水域總面積要在2020年的基礎上增加75%,那么2022年人均綠地面積要比2020年增加多少平方米?
平方米,人口也將隨之增加5萬.這樣,兩江新區2022年的綠地總面積與配套水域總面積要在2020年的基礎上增加75%,那么2022年人均綠地面積要比2020年增加多少平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD在平面直角坐標系中的位置如圖所示,對角線AC與BD的交點E恰好在y軸上,過點D和BC的中點H的直線交AC于點F,線段DE,CD的長是方程x2﹣9x+18=0的兩根,請解答下列問題:
(1)求點D的坐標;
(2)若反比例函數y=![]() (k≠0)的圖象經過點H,則k= ;
(k≠0)的圖象經過點H,則k= ;
(3)點Q在直線BD上,在直線DH上是否存在點P,使以點F,C,P,Q為頂點的四邊形是平行四邊形?若存在,請直接寫出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一個傾斜角為![]() 的斜坡的橫截面,
的斜坡的橫截面,![]() .斜坡頂端B與地面的距離
.斜坡頂端B與地面的距離![]() 為3米.為了對這個斜坡上的綠地進行噴灌,在斜坡底端安裝了一個噴頭A,噴頭A噴出的水珠在空中走過的曲線可以看作拋物線的一部分.設噴出水珠的豎直高度為y(單位:米)(水珠的豎直高度是指水珠與地面的距離),水珠與噴頭A的水平距離為x(單位:米),y與x之間近似滿足函數關系
為3米.為了對這個斜坡上的綠地進行噴灌,在斜坡底端安裝了一個噴頭A,噴頭A噴出的水珠在空中走過的曲線可以看作拋物線的一部分.設噴出水珠的豎直高度為y(單位:米)(水珠的豎直高度是指水珠與地面的距離),水珠與噴頭A的水平距離為x(單位:米),y與x之間近似滿足函數關系![]() (a,b是常數,
(a,b是常數,![]() ),圖2記錄了x與y的相關數據.
),圖2記錄了x與y的相關數據.
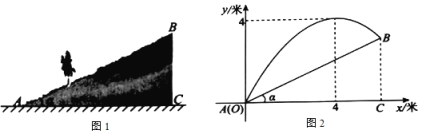
(1)求y關于x的函數關系式;
(2)斜坡上有一棵高1.8米的樹,它與噴頭A的水平距離為2米,通過計算判斷從A噴出的水珠能否越過這棵樹.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com