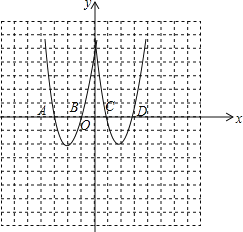
【題目】已知：拋物線
：
與拋物線
關于y軸對稱， 拋物線與x軸分別交于點A（-3， 0）， B（m， 0）， 頂點為M．
（1）求b和m的值；
（2）求拋物線的解析式；
（3）在x軸， y軸上分別有點P（t， 0）， Q（0， -2t）， 其中t＞0， 當線段PQ與拋物線有且只有一個公共點時，求t的取值范圍．
【答案】(1) m=-1；(2) y=2x2-8x+6；(3) 當1≤t＜3或t=
時，PQ與拋物線C2有且僅有一個公共點.
【解析】（1）把A（-3，0）代入y=2x2+bx+6，即可求得b的值，從而求得解析式，令y=0，j解方程即可求得m的值；
（2）根據C1：y=2x2+8x+6=2（x+2）2-2，求得頂點M（-2，-2），即可求得點M關于y軸的對稱點N（2，-2），由于a的值不變，根據頂點得出C2：y=2（x-2）2-2=2x2-8x+6；
（3）根據P、Q的坐標求得直線PQ的解析式，然后分三種情況討論求得．
（1）∵拋物線y=2x2+bx+6過點A（-3，0），
∴0=18-3b+6，
∴b=8，
∴C1：y=2x2+8x+6，
令y=0，則2x2+8x+6=0，
解得x1=-3，x2=-1
∴m=-1；
（2）∵C1：y=2x2+8x+6=2（x+2）2-2，
∴M（-2，-2），
∴點M關于y軸的對稱點N（2，-2），
∴C2：y=2（x-2）2-2=2x2-8x+6，
（3）由題意，點A（-3，0）與D，點B（-1，0）與C關于y軸對稱，
∴D（3，0），C（1，0），
∵P（t，0），Q（0，-2t），
∴PQ：y=2x-2t，
當PQ過點C時，即P與C重合時，t=1，
當PQ過點D時，即P與D重合時，t=3，
當直線PQ與拋物線C2有且僅有一個公共點時，即方程2x2-8x+6=2x-2t中△=0，
方程整理得x2-5x+3+t=0，△=25-4（3+t）=0，
解得t=．
綜上，由圖得，當1≤t＜3或t=時，PQ與拋物線C2有且僅有一個公共點．
科目：初中數學 來源： 題型：
【題目】某中學為推動“時刻聽黨話 永遠跟黨走”校園主題教育活動，計劃開展四項活動：A：黨史演講比賽，B：黨史手抄報比賽，C：黨史知識競賽，D：紅色歌詠比賽．校團委對學生最喜歡的一項活動進行調查，隨機抽取了部分學生，并將調查結果繪制成圖1，圖2兩幅不完整的統計圖．請結合圖中信息解答下列問題：
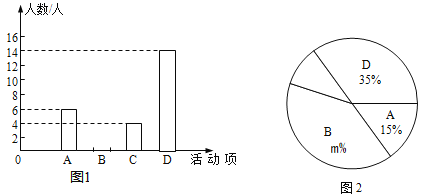
（1）本次共調查了 名學生；將圖1的條形統計圖補充完整；
（2）扇形統計圖中m= ，表示“C”類的扇形的圓心角是 度；
（3）已知在被調查的最喜歡“黨史知識競賽”項目的4個學生中只有1名女生，現從這4名學生中任意抽取2名學生參加該項目比賽，請用畫樹狀圖或列表的方法，求出恰好抽到一名男生一名女生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下表是某校七﹣九年級某月課外興趣小組活動時間統計表，其中各年級同一興趣小組每次活動時間相同，但表格中九年級的兩個數據被遮蓋了，記得九年級文藝小組活動次數與科技小組活動次數相同．
年級 | 課外小組活動總時間（單位：h） | 文藝小組活動次數 | 科技小組活動次數 |
七年級 | 17 | 6 | 8 |
八年級 | 14.5 | 5 | 7 |
九年級 | 12.5 |
|
|
則九年級科技小組活動的次數是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：
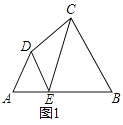
如圖1，在四邊形ABCD的邊AB上任取一點E（點E不與點A、點B重合），分別連接ED，EC，可以把四邊形ABCD分成三個三角形，如果其中有兩個三角形相似，我們就把E叫做四邊形ABCD的邊AB上的相似點；如果這三個三角形都相似，我們就把E叫做四邊形ABCD的邊AB上的強相似點．解決問題：
（1）如圖1，∠A=∠B=∠DEC=55°，試判斷點E是否是四邊形ABCD的邊AB上的相似點，并說明理由；
（2）如圖2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四點均在正方形網格（網格中每個小正方形的邊長為1）的格點（即每個小正方形的頂點）上，試在圖2中畫出矩形ABCD的邊AB上的一個強相似點E；
拓展探究：
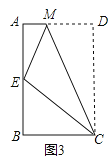
（3）如圖3，將矩形ABCD沿CM折疊，使點D落在AB邊上的點E處．若點E恰好是四邊形ABCM的邊AB上的一個強相似點，試探究AB和BC的數量關系．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠ABC＝90°，AB＝BC，D在邊 AC上，AE⊥BD于 E
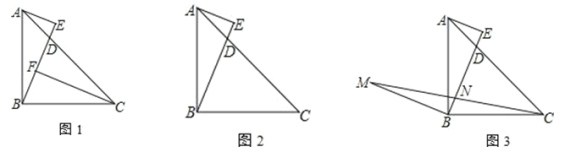
(1)如圖1，作 CF⊥BD于F，求證：CF－AE＝EF
(2)如圖2，若 BC＝CD，求
的值
(3)如圖3，作 BM⊥BE，且 BM＝BE，AE＝2，EN＝4，連 CM交 BE于 N，請直接寫出△BCM的面積為___
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】樂樂對幾何中角平分線的興趣濃厚，請你和樂樂一起探究下面問題吧．已知
°，射線
分別是
和
的平分線；
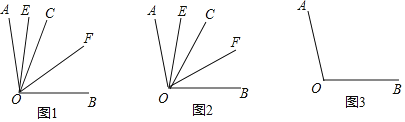
（1）如圖1，若射線
在
的內部，且
，求
的度數；
（2）如圖2，若射線
在的內部繞點
旋轉，則的度數為；
（3）若射線在的外部繞點旋轉(旋轉中，
均指小于
的角)，其余條件不變，請借助圖3探究的大小，請直接寫出的度數(不寫探究過程)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（問題情境）
如圖1，四邊形ABCD是正方形，M是BC邊上的一點，E是CD邊的中點，AE平分∠DAM．求證：AM=AD+MC．
（探究展示）
（2）若四邊形ABCD是長與寬不相等的矩形，其他條件不變，如圖2，試判斷AM=AD+MC是否成立？若成立，請給出證明，若不成立，請說明理由；
（拓展延伸）
（3）若（2）中矩形ABCD兩邊AB=6，BC=9，求AM的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
