
【題目】如圖,在△ABC中,∠ACB=90°,CD是高.
(1)圖中有幾個直角三角形?是哪幾個?
(2)∠1和∠A有什么關系?∠2和∠A呢?還有哪些銳角相等.

【答案】(1)圖中有3個直角三角形,分別是△ACD,△BCD,△ABC.
(2)∠1+∠A=90°,
∠2=∠A,
∠1=∠B.
【解析】試題分析:(1)由題中已知條件∠ACB=90°,CD是高,可以得到∠ADC、∠BDC、∠ACB都是直角。
(2)由(1)得到ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,所以∠1+∠A=90°,∠1+∠2=90°∠B+∠A=90°,由此可以得到∠2=∠A,∠1=∠B。
試題解析:(1) ![]() ∠ACB=90°,CD是高,∴∠ADC=∠BDC=∠ACB=90°∴圖中有3個直角三角形,分別是△ACD,△BCD,△ABC.
∠ACB=90°,CD是高,∴∠ADC=∠BDC=∠ACB=90°∴圖中有3個直角三角形,分別是△ACD,△BCD,△ABC.
(2)∠1+∠A=90°,∠2=∠A,∠1=∠B.
![]() ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,∴∠1+∠A=90°,∠1+∠2=90°,∠B+∠A=90°∴∠2=∠A,∠1=∠B
ACD,△BCD,△ABC是直角三角形,且∠ADC、∠BDC、∠ACB是直角,∴∠1+∠A=90°,∠1+∠2=90°,∠B+∠A=90°∴∠2=∠A,∠1=∠B


科目:初中數學 來源: 題型:
【題目】如圖,是某市一座人行天橋的示意圖,天橋離地面的高BC是10米,坡面10米處有一建筑物HQ,為了方便使行人推車過天橋,市政府部門決定降低坡度,使新坡面DC的傾斜角∠BDC=30°,若新坡面下D處與建筑物之間需留下至少3米寬的人行道,問該建筑物是否需要拆除(計算最后結果保留一位小數).(參考數據:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
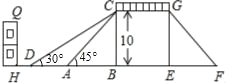
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面的證明(在括號中填寫推理理由) 如圖,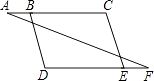
已知∠A=∠F,∠C=∠D,求證:BD∥CE.
證明:因為∠A=∠F,
所以AC∥DF(),
所以∠C+∠=180°().
因為∠C=∠D,
所以∠D+∠=180°(),
所以BD∥CE().
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,EF∥AD,AD∥BC,∠DAC=120°. 
(1)若AB平分∠DAC,求∠ABC的度數.
(2)若∠ACF=20°,求∠BCF的度數.
(3)在(2)的條件下,若CE平分∠BCF,求∠CEF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的圖象,并且C的對應點C′的坐標為(4,1) 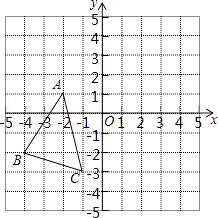
(1)A′、B′兩點的坐標分別為A′、B′;
(2)作出△ABC平移之后的圖形△A′B′C′;
(3)求△A′B′C′的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com