
【題目】如圖,直線![]() 分別交x軸、y軸于A、B兩點,直線BC與x軸交于點
分別交x軸、y軸于A、B兩點,直線BC與x軸交于點![]() ,P是線段AB上的一個動點
,P是線段AB上的一個動點![]() 點P與A、B不重合
點P與A、B不重合![]() .
.

(1)求直線BC所對應的的函數表達式;
(2)設動點P的橫坐標為t,![]() 的面積為S.
的面積為S.
①求出S與t的函數關系式,并寫出自變量t的取值范圍;
②在線段BC上存在點Q,使得四邊形COPQ是平行四邊形,求此時點Q的坐標.
【答案】(1)y=2x+4;(2)①S=-2t+8(0<t<4);②點Q的坐標為(![]() ,
,![]() ).
).
【解析】
(1)根據函數表達式求出點B坐標,結合點C坐標求出BC的表達式;
(2)①根據三角形面積求法可得S與t的表達式;
②過點P作PQ∥x軸,交BC于點Q,得出P和Q的坐標,利用平行四邊形的性質建立方程求解即可.
解:(1)直線y=-x+4與x軸、y軸交點坐標分別為A(4,0)、B(0,4)兩點.
設直線BC所對應的函數關系式為y=kx+4.
∵直線BC經過點C(-2,0),
∴-2k+4=0,解得:k=2,
∴直線BC所對應的函數關系式為y=2x+4.
(2)①由題意,設點P的坐標為(t,-t+4),
∴S=S△POA=![]() ×OA×yP=
×OA×yP=![]() ×4×(-t+4)=-2t+8.
×4×(-t+4)=-2t+8.
即S=-2t+8(0<t<4).
②過點P作PQ∥x軸,交BC于點Q.
∵點P的坐標為(t,-t+4),
∴點Q的坐標為(![]() ,-t+4).
,-t+4).
∵四邊形COPQ是平行四邊形,
∴PQ=OC,即![]() .
.
解得:t=![]() ,
,
∴點Q的坐標為(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】閱讀理解:我們把![]() 稱為二階行列式,規定它的運算法則為
稱為二階行列式,規定它的運算法則為![]() =ad﹣bc,例如:
=ad﹣bc,例如:![]() =2×5﹣3×4=﹣2.
=2×5﹣3×4=﹣2.
(1)填空:若![]() =0,則x= ,
=0,則x= ,![]() >0,則x的取值范圍 ;
>0,則x的取值范圍 ;
(2)若對于正整數m,n滿足,1![]() <3,求m+n的值;
<3,求m+n的值;
(3)若對于兩個非負數x,y,![]() =
=![]() =k﹣1,求實數k的取值范圍.
=k﹣1,求實數k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每個小方格都是邊長為1個單位長度的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,
(1)寫出A、B、C的坐標.
(2)以原點O為中心,將△ABC圍繞原點O逆時針旋轉180°得到△A1B1C1,畫出△A1B1C1.
(3)求(2)中C到C1經過的路徑以及OB掃過的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,CD⊥AB,垂足為D,點E在BC上,EF⊥AB,垂足為F,∠1=∠2.
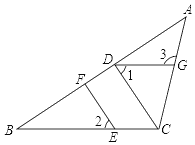
(1)試說明DG∥BC的理由;
(2)如果∠B=34°,且∠ACD=47°,求∠3的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】岳飛是我國古代宋朝的民族英雄,曾任通泰鎮撫史、兼泰州知州.據說在泰州抗擊金兵期間,有一次曾向將領們講了如下一個布陣圖,如圖4是一座城池,在城池的四周設了八個哨所,一共由24個衛士把守,按直線算,每邊都有11個人,后來由于軍情發生變化,連續四次給哨所增添兵力,每次增加4人,但要求在增加人員后,仍然保持每邊11個人把守.請問,兵力應如何調整?
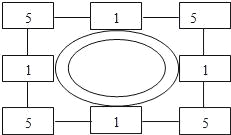
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下面的解題過程的橫線上填空,并在括號內注明理由
.如圖,已知∠A=∠F,∠C=∠D,試說明BD∥CE.

解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代換)
∴BD∥CE( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校研究性學習小組在研究有關二次函數及其圖象性質的問題時,發現了兩個重要結論.一是發現拋物線y=ax2+2x+3(a≠0),當實數a變化時,它的頂點都在某條直線上;二是發現當實數a變化時,若把拋物線y=ax2+2x+3的頂點的橫坐標減少![]() ,縱坐標增加
,縱坐標增加![]() ,得到A點的坐標;若把頂點的橫坐標增加
,得到A點的坐標;若把頂點的橫坐標增加![]() ,縱坐標增加
,縱坐標增加![]() ,得到B點的坐標,則A、B兩點一定仍在拋物線y=ax2+2x+3上.
,得到B點的坐標,則A、B兩點一定仍在拋物線y=ax2+2x+3上.
(1)請你協助探求出當實數a變化時,拋物線y=ax2+2x+3的頂點所在直線的解析式;
(2)問題(1)中的直線上有一個點不是該拋物線的頂點,你能找出它來嗎?并說明理由;
(3)在他們第二個發現的啟發下,運用“一般﹣一特殊﹣一般”的思想,你還能發現什么?你能用數學語言將你的猜想表述出來嗎?你的猜想能成立嗎?若能成立請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將函數y=![]() (x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )
(x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖點P是△ABC的邊BC上的一動點,點E與點P關于直線AB成軸對稱,連接EP交AB于點F,連接AP、EC相交于點O,連接AE.

(1)判斷AE與AP的數量關系,并說明理由.
(2)在點P的運動過程中,當AE∥BC時,判斷AP與BP的數量關系,并說明理由.
(3)若∠BAC=900,點P在運動過程中是否存在線段AP與線段EC互相平分的情況,若存在,請求出點P的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com