
【題目】如圖,在![]() 中,
中,![]() ,
,![]() .動點
.動點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒
以每秒![]() 個單位長度的速度向終點
個單位長度的速度向終點![]() 運動,當點
運動,當點![]() 與點
與點![]() 、
、![]() 不重合時,過點
不重合時,過點![]() 作
作![]() 交折線
交折線![]() 于點
于點![]() ,以
,以![]() 為邊向左作正方形
為邊向左作正方形![]() .設正方形
.設正方形![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() (平方單位),點
(平方單位),點![]() 運動的時間為
運動的時間為![]() (秒).
(秒).
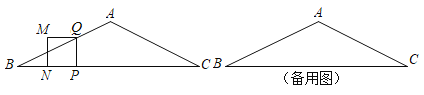
備用圖
(1)用含![]() 的代數式表示
的代數式表示![]() 的長.
的長.
(2)直接寫出點![]() 在
在![]() 內部時
內部時![]() 的取值范圍.
的取值范圍.
(3)求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(4)直接寫出點![]() 落在
落在![]() 的中位線所在直線上時
的中位線所在直線上時![]() 的值.
的值.
【答案】(1)PQ=![]() ;(2)
;(2)![]() ;(3)當
;(3)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)分兩種情況討論:當點Q在線段AB上時,當點Q在線段AC上時;
(2)先計算M在邊AB上時t的值,根據點M在△ABC內部時兩個邊界點即可解答;
(3)分三種情況:
①0<t≤1時,正方形PQMN與△ABC重疊部分圖形是四邊形DNPQ,
②當1<t<![]() 時,正方形PQMN與△ABC重疊部分圖形是五邊形ODNPQ,
時,正方形PQMN與△ABC重疊部分圖形是五邊形ODNPQ,
③當![]() ≤t<2時,正方形PQMN與△ABC重疊部分圖形是正方形MNPQ,
≤t<2時,正方形PQMN與△ABC重疊部分圖形是正方形MNPQ,
分別計算面積即可;
(4)點M落在△ABC的中位線所在直線上時,存在四種情況,畫圖可解答.
解:(1)由題意得:BP=2t,
如圖1,過A作AD⊥BC于D,
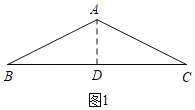
∵AB=AC=![]() ,BC=4,
,BC=4,
∴BD=CD=![]() BC=2,
BC=2,
∴AD=![]() ,
,
∴tan∠B=![]() =
=![]() ,
,
分兩種情況:
①當點Q在線段AB上時,即0<t≤1時,如圖2,
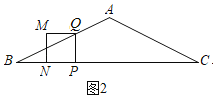
∴tan∠B=![]() ,
,
∴PQ=t;
②當點Q在線段AC上時,即1<t<2時,如圖3,
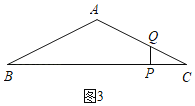
∴tan∠C=tan∠B=![]() =
=![]() ,
,
∴PQ=![]() PC=
PC=![]() =2﹣t;
=2﹣t;
(2)當M在邊AB上時,如圖4,
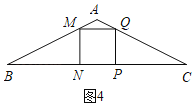
由(1)知:MN=PQ=2﹣t=PN,
tan∠B=![]() =
=![]() ,
,
∴BN=2MN,
∵BP=BN+PN,
∴2t=3MN=3(2﹣t),
t=![]() ,
,
∴點M在△ABC內部時t的取值范圍是![]() <t<2;
<t<2;
(3)分三種情況:
①0<t≤1時,如圖5,正方形PQMN與△ABC重疊部分圖形是四邊形DNPQ,
BP=2t,PQ=PN=MD=t,
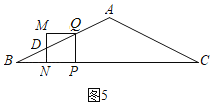
∴BN=2t﹣t=t,
∴DN=![]() t=DM,
t=DM,
∴S=S正方形MNPQ﹣S△MDQ=![]() ;
;
②當1<t<![]() 時,如圖6,正方形PQMN與△ABC重疊部分圖形是五邊形ODNPQ,
時,如圖6,正方形PQMN與△ABC重疊部分圖形是五邊形ODNPQ,
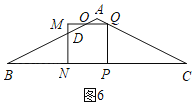
∵PQ=PN=MN=2﹣t,
∴BN=BP﹣PN=2t﹣(2﹣t)=3t﹣2,
∵tan∠B=![]() ,DN=
,DN=![]() BN=
BN=![]() ,
,
∴DM=MN﹣DN=2﹣t﹣![]() =3﹣
=3﹣![]() t,
t,
∵tan∠MOD=tan∠B=![]() =
=![]() ,
,
∴OM=2MD,
∴S=S正方形MNPQ﹣S△MDO=(2﹣t)2﹣![]() =(2﹣t)2﹣
=(2﹣t)2﹣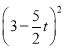 =﹣
=﹣![]() +11t﹣5;
+11t﹣5;
③當![]() ≤t<2時,如圖7,正方形PQMN與△ABC重疊部分圖形是正方形MNPQ,
≤t<2時,如圖7,正方形PQMN與△ABC重疊部分圖形是正方形MNPQ,
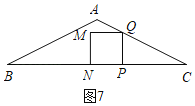
S=PQ2=(2﹣t)2=t2﹣4t+4;
綜上,S與t之間的函數關系式為:S=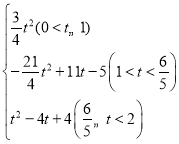 ;
;
(4)存在四種情況:
①如圖8,M在中位線MQ上,則Q是AB的中點,BQ=![]() ,
,
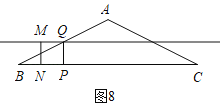
∴BP=1=2t,
t=![]() ;
;
②如圖9,M在中位線MT上,則T是BC的中點,BT=2,

∴MT∥AC,
∴∠C=∠BTM,
∴tan∠BTM=![]() ,
,
∴NT=BP,
∵BP+TN﹣BT=PN,
∴2t+2t﹣2=t,t=![]() ;
;
③如圖10,M在中位線MQ上,
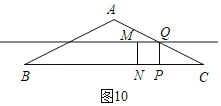
∴Q是AC的中點,
同理得CP=1=4﹣2t,t=![]() ,
,
④如圖11,M在中位線MT上,T是BC的中點,
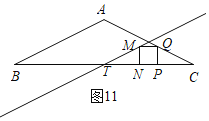
CP=TN=4﹣2t,PQ=PN=2﹣t,
∵CT=TN+PN+PC,
∴2=2(4﹣2t)+2﹣t,
t=![]() ;
;
綜上,t的值是![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.


科目:初中數學 來源: 題型:
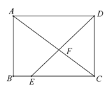
【題目】如圖,在矩形 ABCD 中,E 是邊 BC 邊上一點,連接 DE 交對角線 AC 于點 F,若 AB=6,AD=8,BE=2,則 AF 的長為 _________________ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,其中
兩點,其中![]() ,
,![]() .該拋物線與
.該拋物線與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于另一點
軸交于另一點![]() .
.

(1)求![]() 的值及該拋物線的解析式;
的值及該拋物線的解析式;
(2)如圖2.若點![]() 為線段
為線段![]() 上的一動點(不與
上的一動點(不與![]() 重合).分別以
重合).分別以![]() 、
、![]() 為斜邊,在直線
為斜邊,在直線![]() 的同側作等腰直角△
的同側作等腰直角△![]() 和等腰直角△
和等腰直角△![]() ,連接
,連接![]() ,試確定△
,試確定△![]() 面積最大時
面積最大時![]() 點的坐標.
點的坐標.
(3)如圖3.連接![]() 、
、![]() ,在線段
,在線段![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() 為頂點的三角形與△
為頂點的三角形與△![]() 相似,若存在,請直接寫出點
相似,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
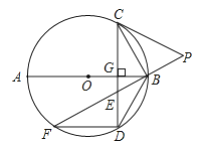
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 于點
于點![]() ,
,![]() 是
是![]() 上一點,且
上一點,且![]() ,延長
,延長![]() 至點
至點![]() ,連接
,連接![]() ,使
,使![]() ,延長
,延長![]() 與
與![]() 交于點
交于點![]() ,連結
,連結![]() ,
,![]() .
.
(1)連結![]() ,求證:
,求證:![]() ;
;
(2)求證:![]() 是
是![]() 的切線;
的切線;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
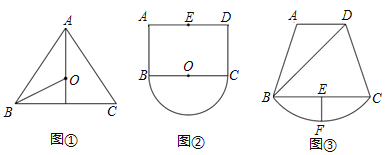
【題目】問題提出
(1)如圖①,在△ABC中,AB=AC=10,BC=12,點O是△ABC的外接圓的圓心,則OB的長為
問題探究
(2)如圖②,已知矩形ABCD,AB=4,AD=6,點E為AD的中點,以BC為直徑作半圓O,點P為半圓O上一動點,求E、P之間的最大距離;
問題解決
(3)某地有一塊如圖③所示的果園,果園是由四邊形ABCD和弦CB與其所對的劣弧場地組成的,果園主人現要從入口D到![]() 上的一點P修建一條筆直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一點P修建一條筆直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,過弦BC的中點E作EF⊥BC交
米,BC=160米,過弦BC的中點E作EF⊥BC交![]() 于點F,又測得EF=40米.修建小路平均每米需要40元(小路寬度不計),不考慮其他因素,請你根據以上信息,幫助果園主人計算修建這條小路最多要花費多少元?
于點F,又測得EF=40米.修建小路平均每米需要40元(小路寬度不計),不考慮其他因素,請你根據以上信息,幫助果園主人計算修建這條小路最多要花費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】日照間距系數反映了房屋日照情況.如圖①,當前后房屋都朝向正南時,日照間距系數=L:(H﹣H1),其中L為樓間水平距離,H為南側樓房高度,H1為北側樓房底層窗臺至地面高度.
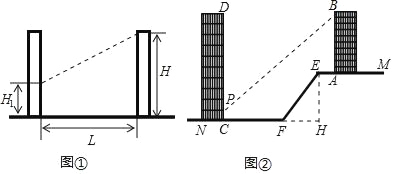
如圖②,山坡EF朝北,EF長為15m,坡度為i=1:0.75,山坡頂部平地EM上有一高為22.5m的樓房AB,底部A到E點的距離為4m.
(1)求山坡EF的水平寬度FH;
(2)欲在AB樓正北側山腳的平地FN上建一樓房CD,已知該樓底層窗臺P處至地面C處的高度為0.9m,要使該樓的日照間距系數不低于1.25,底部C距F處至少多遠?
查看答案和解析>>
科目:初中數學 來源: 題型:
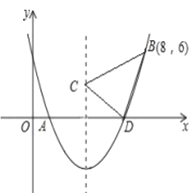
【題目】如圖,二次函數![]() 的圖象交
的圖象交![]() 軸于
軸于![]() 兩點,并經過
兩點,并經過![]() 點,已知
點,已知![]() 點坐標是
點坐標是![]() ,
,![]() 點坐標是
點坐標是![]() .
.
(1)求二次函數的解析式;
(2)求函數圖象的頂點坐標及![]() 點的坐標;
點的坐標;
(3)二次函數的對稱軸上是否存在一點![]() ,使得
,使得![]() 的周長最小?若
的周長最小?若![]() 點存在,求出
點存在,求出![]() 點的坐標,若
點的坐標,若![]() 點不存在,請說明理由.
點不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司計劃購買2臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元,三年后如果備件多余,每個以![]() 元(
元(![]() )回收.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得到如下頻數分布直方圖:
)回收.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得到如下頻數分布直方圖:
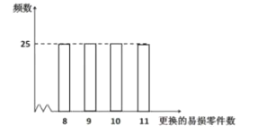
記![]() 表示2臺機器三年內共需更換的易損零件數,
表示2臺機器三年內共需更換的易損零件數,![]() 表示購買2臺機器的同時購買的易損零件數.
表示購買2臺機器的同時購買的易損零件數.
(1)以100臺機器為樣本,請利用畫樹狀圖或列表的方法估計![]() 不超過19的概率;
不超過19的概率;
(2)以這100臺機器在購買易損零件上所需費用的平均數為決策依據,在![]() 與
與![]() 之中選其一,當
之中選其一,當![]() 為何值時,選
為何值時,選![]() 比較劃算?
比較劃算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形OABC的一個頂點O是平面直角坐標系的原點,頂點A,C分別在y軸和x軸上,P為邊OC上的一個動點,且PQ⊥BP,PQ=BP,當點P從點C運動到點O時,可知點Q始終在某函數圖象上運動,則其函數圖象是( )
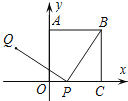
A.線段B.圓弧
C.雙曲線的一部分D.拋物線的一部分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com