
【題目】如圖,四邊形![]() 內接于⊙
內接于⊙![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,過點
,過點![]() 作⊙
作⊙![]() 的切線,分別交
的切線,分別交![]() ,
,![]() 的延長線于點
的延長線于點![]() ,
,![]() .
.
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
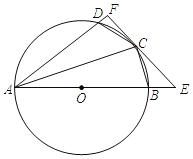
【答案】(1)證明見解析;(2)AD![]() ,詳情見解析;
,詳情見解析;
【解析】
(1)連接OC,如圖,先證明OC∥AF,再根據切線的性質得OC⊥EF,從而得到AF⊥EF;
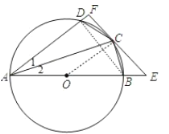
(2)先利用OC∥AF得到∠COE=∠DAB,在Rt△OCE中,設OC=r,利用余弦的定義得到![]() ,解得r=4,連接BD,如圖,根據圓周角定理得到∠ADB=90°,然后根據余弦的定義可計算出AD的長.
,解得r=4,連接BD,如圖,根據圓周角定理得到∠ADB=90°,然后根據余弦的定義可計算出AD的長.
(1)證明:連接OC,
∵CD=BD,
∴弧CD=弧BC,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠OCA,
∴∠1=∠OCA,
∴OC∥AF,
∵EF為切線,
∴OC⊥EF,
∴AF⊥EF;
(2)∵OC∥AF,
∴∠COE=∠DAB,
在Rt△OCE中,設OC=r,
∵cos∠COE=cos∠DAB=![]() ,
,
即![]() ,
,
解得r=4,
連接BD,如圖,
∵AB為直徑,
∴∠ADB=90°,
在Rt△ADB中,cos∠DAB=![]() ,
,
∴AD![]() ;
;


 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案科目:初中數學 來源: 題型:
【題目】閱讀下面材料:在數學課上,老師提出如下問題:
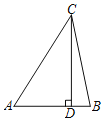
已知:如圖,CD是△ABC的高,
尺規(guī)作圖:在線段CD上求作點P,使∠APB=45°(保留作圖痕跡,寫出作法),
請回答:你推出∠APB=45°的依據是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
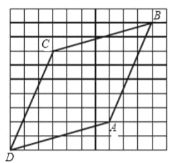
【題目】在小正方形組成網格圖中,四邊形 ABCD 的頂點都在格點上,如圖所示.則下列結論錯 誤的是( )
A.![]() B.
B.![]()
C.四邊形![]() 是菱形D.將邊
是菱形D.將邊![]() 向右平移
向右平移![]() 格,再向上平移
格,再向上平移![]() 格就與邊
格就與邊![]() 重合
重合
查看答案和解析>>
科目:初中數學 來源: 題型:
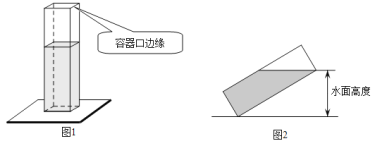
【題目】如圖1,長、寬均為3,高為8的長方體容器,放置在水平桌面上,里面盛有水,水面高為6,繞底面一棱長進行旋轉傾斜后,水面恰好觸到容器口邊緣,圖2是此時的示意圖,則圖2中水面高度為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系![]() 中的點
中的點![]() 和
和![]() (半徑為
(半徑為![]() ),給出如下定義:若點
),給出如下定義:若點![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,且
,且![]() ,則稱點
,則稱點![]() 為
為![]() 的稱心點.
的稱心點.
(1)當![]() 的半徑為2時,
的半徑為2時,
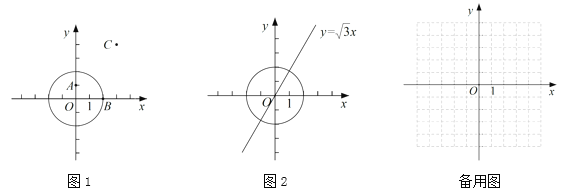
①如圖1,在點![]() ,
,![]() ,
,![]() 中,
中,![]() 的稱心點是 ;
的稱心點是 ;
②如圖2,點![]() 在直線
在直線![]() 上,若點
上,若點![]() 是
是![]() 的稱心點,求點
的稱心點,求點![]() 的橫坐標
的橫坐標![]() 的取值范圍;
的取值范圍;
(2)![]() 的圓心為
的圓心為![]() ,半徑為2,直線
,半徑為2,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,
,![]() .若線段
.若線段![]() 上的所有點都是
上的所有點都是![]() 的稱心點,直接寫出
的稱心點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
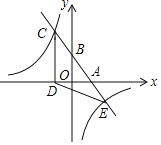
【題目】如圖,一次函數y=kx+b(k、b為常數,k≠0)的圖象與x軸、y軸分別交于A、B兩點,且與反比例函數y=![]() (n為常數,且n≠0)的圖象在第二象限交于點C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(n為常數,且n≠0)的圖象在第二象限交于點C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(1)求一次函數與反比例函數的解析式;
(2)記兩函數圖象的另一個交點為E,求△CDE的面積;
(3)直接寫出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現今“微信運動”被越來越多的人關注和喜愛,某數學興趣小組隨機調查了我市![]() 名教師某日“微信運動”中的步數情況進行統(tǒng)計整理,繪制了如下的統(tǒng)計圖表(不完整):
名教師某日“微信運動”中的步數情況進行統(tǒng)計整理,繪制了如下的統(tǒng)計圖表(不完整):
步數 | 頻數 | 頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

請根據以上信息,解答下列問題:
(1)寫出![]() ,
,![]() ,
,![]() ,
,![]() 的值并補全頻數分布直方圖;
的值并補全頻數分布直方圖;
(2)我市約有![]() 名教師,用調查的樣本數據估計日行走步數超過
名教師,用調查的樣本數據估計日行走步數超過![]() 步(包含
步(包含![]() 步)的教師有多少名?
步)的教師有多少名?
(3)若在![]() 名被調查的教師中,選取日行走步數超過
名被調查的教師中,選取日行走步數超過![]() 步(包含
步(包含![]() 步)的兩名教師與大家分享心得,用樹形圖或列表法求被選取的兩名教師恰好都在
步)的兩名教師與大家分享心得,用樹形圖或列表法求被選取的兩名教師恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館共有80間客房.賓館負責人根據經驗作出預測:今年7月份,每天的房間空閑數y(間)與定價x(元/間)之間滿足y=![]() x﹣42(x≥168).若賓館每天的日常運營成本為5000元,有客人入住的房間,賓館每天每間另外還需支出28元的各種費用,賓館想要獲得最大利潤,同時也想讓客人得到實惠,應將房間定價確定為( )
x﹣42(x≥168).若賓館每天的日常運營成本為5000元,有客人入住的房間,賓館每天每間另外還需支出28元的各種費用,賓館想要獲得最大利潤,同時也想讓客人得到實惠,應將房間定價確定為( )
A.252元/間B.256元/間C.258元/間D.260元/間
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com