
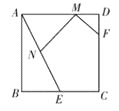
【題目】如圖,在正方形ABCD中,AB=4,E是BC邊的中點, F是CD邊上的一點, 且DF=1.若M、N分別是線段AD、AE上的動點,則MN+MF的最小值為________.
【答案】![]()
【解析】
作點F關于AD的對稱點G,過點G作GN⊥AE于點N,交AD于點M,可證得MG=MF,△MDG≌△MDF,DF=DG=1 ,可推出MN+MF=NG,根據垂線段最短,可知此時MN+MF的最小值就是NG的長;利用正方形的性質,可求出BE的長,同時可以推出∠B=∠ANM=∠FDM,∠AMN=∠BAE=∠FMD,再利用有兩組對應角相等的三角形相似,可證得△ABE∽△MNA∽△FMD,然后利用相似三角形的性質及勾股定理就可求出MN,MG的長,由此看求出NG的長.
作點F關于AD的對稱點G,過點G作GN⊥AE于點N,交AD于點M,
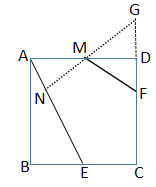
∴MG=MF,△MDG≌△MDF,DF=DG=1
∴∠GMD=∠DMF
∴MN+MF=MN+MG=NG
根據垂線段最短,可知此時MN+MF的最小值就是NG的長.
∵正方形BCD,點E是BC的中點
∴BE=![]() BC=
BC=![]() AB=2
AB=2
∴∠B=∠ANM=∠FDM=90°,∠BAE+∠MAN=90°,
∵∠AMN+∠MAN=90°,
∴∠AMN=∠BAE,
∵∠AMN=∠DMG
∴∠AMN=∠BAE=∠FMD
∴△ABE∽△MNA∽△FMD
∴![]() 即
即![]()
解之:MD=2,
∴AM=AD-MD=4-2=2
∴![]()
設AN=x,則MN=2x
∴AN2+MN2=AM2,
∴x2+4x2=4
解之:AN=x=![]()
∴MN=2AN=![]() ;
;
在Rt△MDG中,MG=![]()
∴NG=MN+MG=![]() .
.
故答案為:![]() .
.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:
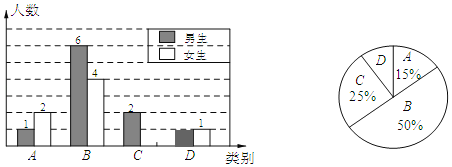
【題目】李老師為了解某校學生完成數學課前預習的具體情況,對部分學生進行了跟蹤調查,并將調查結果分為四類,A:很好;B:較好;C:一般;D:較差.繪制成如下統計圖.
(1)李老師一共調查了多少名同學?并將下面條形統計圖補充完整.
(2)若該校有1000名學生,則數學課前預習“很好”和“較好”總共約多少人?
(3)為了共同進步,李老師想從被調查的A類和D類學生中各隨機選取一位同學進行“一幫一”互助學習,求出所選兩位同學恰好是一位男同學和一位女同學的概率.(要求列表或樹狀圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() ,
,![]() ,點
,點![]() 是
是![]() 軸上點
軸上點![]() 右側一點,以
右側一點,以![]() ,
,![]() 為兩邊的菱形
為兩邊的菱形![]() 的頂點
的頂點![]() 落在反比例函數
落在反比例函數![]() 的圖象上.
的圖象上.
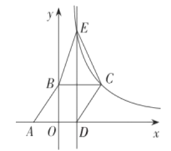
(1)求反比例函數的表達式;
(2)過點![]() 作
作![]() 軸的垂線,交反比例函數的圖象于點
軸的垂線,交反比例函數的圖象于點![]() ,連接
,連接![]() ,
,![]() ,求
,求![]() 的面積:
的面積:
(3)當![]() 時,請直接寫出
時,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在正方形![]() 中,
中,![]() 在
在![]() 上從
上從![]() 向
向![]() 運動,連接
運動,連接![]() 交
交![]() 于
于![]() 連接
連接![]() .
.
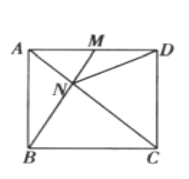
(1)證明:無論![]() 運動到
運動到![]() 上的何處,都有
上的何處,都有![]() ;
;
(2)當![]() 運動到何處時,
運動到何處時,![]() ?
?
(3)若![]() 從
從![]() 到
到![]() 再從
再從![]() 到
到![]() ,在整個運動過程中,
,在整個運動過程中,![]() 為多少時,
為多少時,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】上周六上午![]() 點,小穎同爸爸媽媽一起從西安出發回安康看望姥姥,途中他們在一個服務區休息了半小時,然后直達姥姥家,如圖,是小穎一家這次行程中距姥姥家的距離
點,小穎同爸爸媽媽一起從西安出發回安康看望姥姥,途中他們在一個服務區休息了半小時,然后直達姥姥家,如圖,是小穎一家這次行程中距姥姥家的距離![]() (千米)與他們路途所用的時間
(千米)與他們路途所用的時間![]() (時)之間的函數圖象,請根據以上信息,解答下列問題:
(時)之間的函數圖象,請根據以上信息,解答下列問題:
(1)求直線![]() 所對應的函數關系式;
所對應的函數關系式;
(2)已知小穎一家出服務區后,行駛![]() 分鐘時,距姥姥家還有
分鐘時,距姥姥家還有![]() 千米,問小穎一家當天幾點到達姥姥家?
千米,問小穎一家當天幾點到達姥姥家?
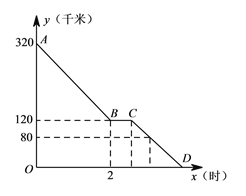
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】文具店有三種品牌的6個筆記本,價格是4,5,7(單位:元)三種,從中隨機拿出一個本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求這6個本價格的眾數.
(2)若琪琪已拿走一個7元本,嘉嘉準備從剩余5個本中隨機拿一個本.
①所剩的5個本價格的中位數與原來6個本價格的中位數是否相同?并簡要說明理由;
②嘉嘉先隨機拿出一個本后不放回,之后又隨機從剩余的本中拿一個本,用列表法求嘉嘉兩次都拿到7元本的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校準備組織一次“研學之旅”活動,現用抽簽的方式從以下四個地方:九峰公園、柑橘博覽園、平田桐樹坑、長潭水庫(其中九峰公園、平田桐樹坑是愛國主義教育基地)中確定兩個作為活動地點.將四個地點分別寫在4張完全相同的卡片上,背面朝上并洗勻,先從中隨機抽取一張卡片,再從剩下的卡片中隨機抽取一張.則“抽中的兩個地方都是愛國主義教育基地”的概率為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚中華優秀傳統文化,某校組織了“古詩詞”知識競賽,由九年級的若干名學生參加選拔賽,從中選出10名優勝者,下面是對參賽學生成績的不完整統計.
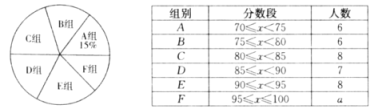
(1)統計表中,![]() =_____;各組人數的中位數是_____;統計圖中,
=_____;各組人數的中位數是_____;統計圖中,![]() 組所在扇形的圓心角是_____°;
組所在扇形的圓心角是_____°;
(2)李明同學得了88分,他說自己在參加選拔賽的同學中屬于中午偏上水平,你認為他說的有道理嗎?為什么?
(3)選出的10名優勝者中,男生、女生的分布情況如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人數 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人數 | 1 | 0 | 0 | 2 | 1 | 1 |
若從中任選1名男生和1名女生代表學校參加全區的比賽,請有列表法或畫樹狀圖法求男生和女生都出在四班的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com