
【題目】已知二次函數y=ax2+bx+6的圖像開口向下,與x軸交于點A(-6,0)和點B(2,0),與y軸交于點C,點P是該函數圖像上的一個動點(不與點C重合)

(1) 求二次函數的關系式;
(2)如圖1當點P是該函數圖像上一個動點且在線段![]() 的上方,若△PCA的面積為12,求點P的坐標;
的上方,若△PCA的面積為12,求點P的坐標;
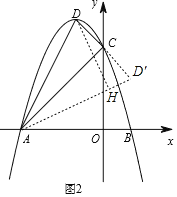
(3)如圖2,該函數圖像的頂點為D,在該函數圖像上是否存在點E,使得∠EAB=2∠DAC,若存在請直接寫出點E的坐標;若不存在請說明理由.
【答案】(1) ![]() ;(2)(﹣2,8)或(﹣4,6);(3)
;(2)(﹣2,8)或(﹣4,6);(3) ![]()
![]() 或
或![]() .
.
【解析】
(1)由題意設函數的表達式為:![]() 結合已知函數解析式即可求解;
結合已知函數解析式即可求解;
(2)由點P在線段![]() 的上方,設
的上方,設![]() 連接
連接![]()
![]() ,從而可得答案;
,從而可得答案;
(3)證明![]() 為直角三角形,延長DC至D′使CD=CD′,連接AD′,過點D作DH⊥AD′,計算sin∠DAC ,sin2∠DAC=sin∠DAD′得到sin∠EAB,tan∠EAB ,利用一次函數的性質得一次函數是解析式,聯立解析式解方程組即可求解.
為直角三角形,延長DC至D′使CD=CD′,連接AD′,過點D作DH⊥AD′,計算sin∠DAC ,sin2∠DAC=sin∠DAD′得到sin∠EAB,tan∠EAB ,利用一次函數的性質得一次函數是解析式,聯立解析式解方程組即可求解.
解:(1)![]() 拋物線與x軸交于點A(-6,0)和點B(2,0),
拋物線與x軸交于點A(-6,0)和點B(2,0),
![]() 設函數的表達式為:
設函數的表達式為:![]()
![]() 二次函數
二次函數![]()
![]()
解得:![]()
![]() 函數的表達式為:
函數的表達式為:![]() .
.
(2)如圖1所示,![]() 在
在![]() 的上方,
的上方,
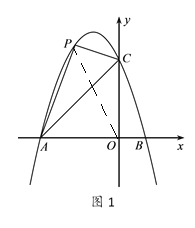
連接![]()
![]()
設![]()
把![]() 代入
代入![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
解得:![]()
所以點P坐標為![]() 或
或![]()
(3)![]() 拋物線為:
拋物線為:![]() ,
,![]() 為頂點,
為頂點,
![]()
![]()
![]()
則![]()
![]()
![]()
![]()
![]()
延長DC至D′使CD=CD′,連接AD′,
過點D作DH⊥AD′, 則![]()
![]()
即:![]()
解得:![]()

![]() ∠EAB=2∠DAC,
∠EAB=2∠DAC,
![]()
①當點E在AB上方時, 則直線AE的表達式為:![]() ,
,
將點![]() 坐標代入上式:
坐標代入上式:![]()
![]()
直線AE的表達式為:![]()

解得: 或
或![]() (舍去)
(舍去)
即點![]()
②當點E在AB下方時,![]()
設直線![]() 為:
為:![]()
將點![]() 坐標代入上式:
坐標代入上式:![]()
![]()
![]() 直線
直線![]() 為:
為:![]()
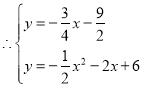
解得: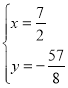 或
或![]() (舍去)
(舍去)
![]()
綜上,點![]() 或
或![]()


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:初中數學 來源: 題型:
【題目】某企業承接了27000件產品的生產任務,計劃安排甲、乙兩個車間的共50名工人,合作生產20天完成.已知甲、乙兩個車間利用現有設備,工人的工作效率為:甲車間每人每天生產25件,乙車間每人每天生產30件.
(1)求甲、乙兩個車間各有多少名工人參與生產?
(2)為了提前完成生產任務,該企業設計了兩種方案:
方案一 甲車間租用先進生產設備,工人的工作效率可提高20%,乙車間維持不變.
方案二 乙車間再臨時招聘若干名工人(工作效率與原工人相同),甲車間維持不變.
設計的這兩種方案,企業完成生產任務的時間相同.
①求乙車間需臨時招聘的工人數;
②若甲車間租用設備的租金每天900元,租用期間另需一次性支付運輸等費用1500元;乙車間需支付臨時招聘的工人每人每天200元.問:從新增加的費用考慮,應選擇哪種方案能更節省開支?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
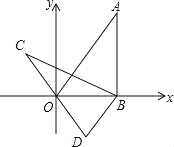
【題目】如圖,在平面直角坐標系xOy中,直線y=![]() x經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD,若點B的坐標為(2,0),則點C的坐標為 .
x經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD,若點B的坐標為(2,0),則點C的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
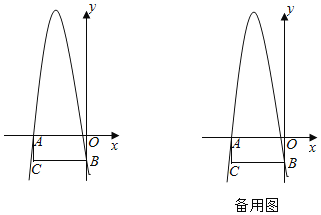
【題目】如圖,在平面直角坐標系中,矩形AOBC的邊AO在x軸的負半軸上,邊OB在y軸的負半軸上.且AO=12,OB=9.拋物線y=﹣x2+bx+c經過點A和點B.
(1)求拋物線的表達式;
(2)在第二象限的拋物線上找一點M,連接AM,BM,AB,當△ABM面積最大時,求點M的坐標;
(3)點D是線段AO上的動點,點E是線段BO上的動點,點F是射線AC上的動點,連接EF,DF,DE,BD,且EF是線段BD的垂直平分線.當CF=1時.
①直接寫出點D的坐標 ;
②若△DEF的面積為30,當拋物線y=﹣x2+bx+c經過平移同時過點D和點E時,請直接寫出此時的拋物線的表達式 .
查看答案和解析>>
科目:初中數學 來源: 題型:
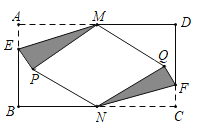
【題目】如圖, 在矩形紙片![]() 中,
中, ![]() , 點
, 點![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點, 點
的中點, 點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上, 且
上, 且![]() .將
.將![]() 沿
沿![]() 折疊, 點
折疊, 點![]() 的對應點為點
的對應點為點![]() ,將
,將![]() 沿
沿![]() 折疊, 點
折疊, 點![]() 的對應點為點
的對應點為點![]() ,當四邊形
,當四邊形![]() 為菱形時, 則
為菱形時, 則![]() _______.
_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
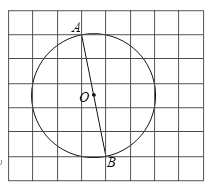
【題目】如圖,在每個小正方形的邊長為![]() 的網格中,點
的網格中,點![]() ,點
,點![]() 均落在格點上,
均落在格點上,![]() 為⊙
為⊙![]() 的直徑.
的直徑.
(1)![]() 的長等于__________;
的長等于__________;
(2)請在如圖所示的網格中,用無刻度的直尺,畫出一個以![]() 為斜邊、面積為
為斜邊、面積為![]() 的
的![]() ,并簡要說明點
,并簡要說明點![]() 的位置是如何找到的(不要求證明)__________.
的位置是如何找到的(不要求證明)__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
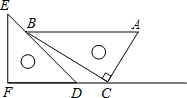
【題目】三角板是我們學習數學的好幫手.將一對直角三角板如圖放置,點C在FD的延長線上,點B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,則CD的長度是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com