
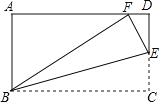
【題目】如圖,在矩形![]() 中,
中,![]() ,在
,在![]() 上任取一點
上任取一點![]() ,連接
,連接![]() .將
.將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 恰好落在
恰好落在![]() 邊上的點
邊上的點![]() 處,則
處,則![]() 的面積為_______.
的面積為_______.
【答案】![]()
【解析】
設CE=x,由矩形的性質得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折疊的性質得出BF=BC=5,EF=CE=x,DE=CD-CE=3-x.在Rt△ABF中利用勾股定理求出AF的長度,進而求出DF的長度;然后在Rt△DEF根據勾股定理列出關于x的方程即可求出CE,再利用三角形面積求解.
解:設CE=x.
∵四邊形ABCD是矩形,
∴AD=BC=5,CD=AB=3,∠A=∠D=90°.
∵將△BCE沿BE折疊,使點C恰好落在AD邊上的點F處,
∴BF=BC=5,EF=CE=x,DE=CD-CE=3-x.
在Rt△ABF中,由勾股定理得:
AF2=52-32=16,
∴AF=4,DF=5-4=1.
在Rt△DEF中,由勾股定理得:
EF2=DE2+DF2,
即x2=(3-x)2+12,
解得:x=![]() ,
,
∴DE=![]()
∴S△EDF=![]()


科目:初中數學 來源: 題型:
【題目】以下是兩張不同類型火車的車票(“![]() 次”表示動車,“
次”表示動車,“![]() 次”表示高鐵):
次”表示高鐵):
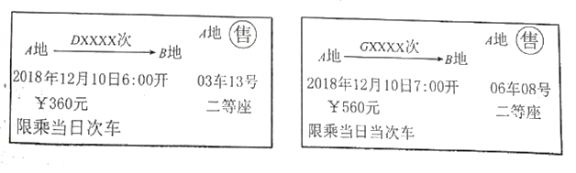
![]() 根據車票中的信息填空:該列動車和高鐵是 向而行(填“相”或“同”).
根據車票中的信息填空:該列動車和高鐵是 向而行(填“相”或“同”).
![]() 已知該動車和高鐵的平均速度分別為
已知該動車和高鐵的平均速度分別為![]() ,兩列火車的長度不計.經過測算,如果兩列火車直達終點(即中途都不停靠任何站點),高鐵比動車將早到2
,兩列火車的長度不計.經過測算,如果兩列火車直達終點(即中途都不停靠任何站點),高鐵比動車將早到2![]() .求
.求![]() 兩地之間的距離.
兩地之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y關于x的二次函數y=ax2﹣bx+2(a≠0).
(1)當a=﹣2,b=﹣4時,求該函數圖象的對稱軸及頂點坐標.
(2)在(1)的條件下,Q(m,t)為該函數圖象上的一點,若Q關于原點的對稱點P也落在該函數圖象上,求m的值.
(3)當該函數圖象經過點(1,0)時,若A(![]() ,y1),B(
,y1),B(![]() ,y2)是該函數圖象上的兩點,試比較y1與y2的大小.
,y2)是該函數圖象上的兩點,試比較y1與y2的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 為其內部一條射線.
為其內部一條射線.
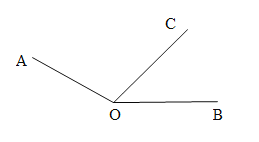
(1)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() .求
.求![]() 的度數;
的度數;
(2)若![]() ,射線
,射線![]() 從
從![]() 起繞著
起繞著![]() 點順時針旋轉,旋轉的速度是
點順時針旋轉,旋轉的速度是![]() 每秒鐘,設旋轉的時間為
每秒鐘,設旋轉的時間為![]() ,試求當
,試求當![]()
![]()
![]()
![]() 時
時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,過點B(6,0)的直線AB與![]() 軸相交于點C(0,6),與直線OA相交于點A且點A縱坐標為2,動點P沿路線O
軸相交于點C(0,6),與直線OA相交于點A且點A縱坐標為2,動點P沿路線O![]() A
A![]() C運動.
C運動.
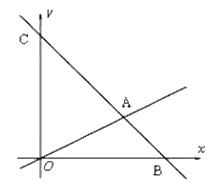
(1)求直線BC的解析式.
(2)求![]() 的面積.
的面積.
(3)當![]() 的面積是
的面積是![]() 的面積的
的面積的![]() 時,求出這時點P的坐標.
時,求出這時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數C1:![]() (m>0)的圖象與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
(m>0)的圖象與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
(1)求點A和點C的坐標;
(2)當AB=4時,
①求二次函數C1的表達式;
②在拋物線的對稱軸上是否存在點D,使△DAC的周長最小,若存在,求出點D的坐標,若不存在,請說明理由;
(3)將(2)中拋物線C1向上平移n個單位,得到拋物線C2,若當0≤x≤![]() 時,拋物線C2與x軸只有一個公共點,結合函數圖象,求出n的取值范圍.
時,拋物線C2與x軸只有一個公共點,結合函數圖象,求出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學小組的同學為了解學生每周閱讀的時間,隨機調查了50名同學,繪制了如圖所示的統計圖,這組數據的中位數和眾數分別是( )
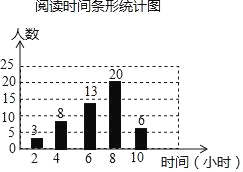
A. 中位數是25人,眾數是20人 B. 中位數和眾數都是8小時
C. 中位數是13人,眾數是20人 D. 中位數是6小時,眾數是8小時
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com