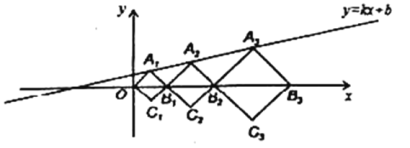
【題目】在平面直角坐標系
中，正方形
、
、
，…，按圖所示的方式放置.點
、
、
，…和點
、
、
，…分別在直線
和
軸上.已知
，
，則點的坐標是______.
【答案】
【解析】
由正方形的軸對稱性，由C1、C2的坐標可求A1、A2的坐標，將A1、A2的坐標代入y=kx+b中，得到關于k與b的方程組，求出方程組的解得到k與b的值，從而求直線解析式，由正方形的性質求出OB1，OB2的長，設B2G=A3G=t，表示出A3的坐標，代入直線方程中列出關于b的方程，求出方程的解得到b的值，確定出A3的坐標．
連接A1C1，A2C2，A3C3，分別交x軸于點E、F、G，
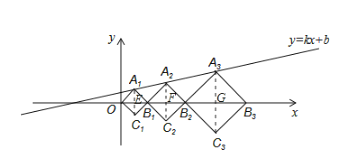
∵正方形A1B1C1O、A2B2C2B1、A3B3C3B2，
∴A1與C1關于x軸對稱，A2與C2關于x軸對稱，A3與C3關于x軸對稱，
∵C1（1，-1），C2（
，
），
∴A1（1，1），A2（，），
∴OB1=2OE=2，OB2=OB1+2B1F=2+2×（-2）=5，
將A1與A2的坐標代入y=kx+b中得：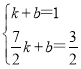
，
解得：
，
∴直線解析式為y=
x+
，
設B2G=A3G=t，則有A3坐標為（5+t，t），
代入直線解析式得：t=（5+t）+，
解得：t=
，
∴A3坐標為.
故答案是：.
科目：初中數學 來源： 題型：
【題目】長沙市文化底蘊深厚，旅游資源豐富，天心閣、岳麓山、橘子洲三個景區是人們節假日游玩的熱點景區，李老師對九年級1班學生五一長假隨父母到這三個景區游玩的計劃做了全面調查，調查分四個類別：A、游三個景區；B、游兩個景區；C、游一個景區；D、不到這三個景區游玩．現根據調查結果繪制了不完整的條形統計圖和扇形統計圖，請結合圖中信息解答下列問題：
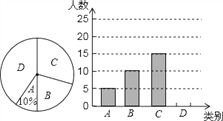
（1）九(1)班共有學生 人，請將條形統計圖補充完整；
（2）在扇形統計圖中，表示“B類別”的扇形的圓心角的度數為 ；
（3）若小明、小華兩名同學，各自從三個景區中隨機選一個作為5月1日游玩的景區，請用列表或者畫樹狀圖的形式求出他們同時選中岳麓山的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算
（1）33.1﹣10.7﹣（﹣229）﹣|﹣
|
（2）
（3）（﹣36）×
（4）4﹣（﹣2）
（5）﹣3﹣[﹣5+（1﹣2×
）÷（﹣2）]
（6）（﹣96）×（﹣0.125）+96×
+（﹣96）×
（7）﹣14+（﹣3）×[（﹣4）2+2]﹣（﹣2）3÷4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為解方程（x2﹣1）2﹣5（x2﹣1）+4=0，我們可以將x2﹣1視為一個整體，然后設x2﹣1=y，則
（x2﹣1）=y2，原方程化為y2﹣5y+4=0．①
解得y1=1，y2=4
當y=1時，x2﹣1=1．∴x2=2．∴x=±
；
當y=4時，x2﹣1=4，∴x2=5，∴x=±
．
∴原方程的解為x1=
，x2=﹣
，x3=
，x4=﹣
解答問題：
（1）填空：在由原方程得到方程①的過程中，利用 法達到了降次的目的，體現了 的數學思想．
（2）解方程：x4﹣x2﹣6=0．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】探究題：如圖，用同樣大小的黑色棋子按如圖所示的規律擺放，它們的棋子數依次表示為 a1，a2，a3，a4，…，an．
…
請你認真觀察上面四個圖案，從中發現規律，并試著解答下列問題：
（1）寫出 a1，a2，a3，a4 的值；
（2）求 a7 的值；
（3）用 n 表示出 an，并判斷第幾個圖案有 6055 個黑色棋子．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(9分)已知：
ABCD的兩邊AB，AD的長是關于x的方程
的兩個實數根．
（1）當m為何值時，四邊形ABCD是菱形？求出這時菱形的邊長；
（2）若AB的長為2，那么ABCD的周長是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
