
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉(zhuǎn)得到
順時針旋轉(zhuǎn)得到![]() ,當(dāng)點
,當(dāng)點![]() 、
、![]() 、
、![]() 三點共線時,旋轉(zhuǎn)角為
三點共線時,旋轉(zhuǎn)角為![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,下面結(jié)論:①
,下面結(jié)論:①![]() 為等腰三角形;②
為等腰三角形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 中,正確結(jié)論的個數(shù)是( )
中,正確結(jié)論的個數(shù)是( )
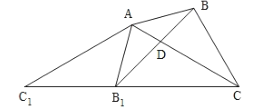
A.2個B.3個C.4個D.5個
【答案】C
【解析】
首先根據(jù)旋轉(zhuǎn)性質(zhì)得出![]() ,從而對結(jié)論①進(jìn)行判斷,然后通過對三角形內(nèi)部角度之間的計算進(jìn)一步對結(jié)論④進(jìn)行判斷,再后通過證明∠
,從而對結(jié)論①進(jìn)行判斷,然后通過對三角形內(nèi)部角度之間的計算進(jìn)一步對結(jié)論④進(jìn)行判斷,再后通過證明∠![]() =∠BDC,∠
=∠BDC,∠![]() =∠BCD對結(jié)論②進(jìn)行判斷,再者進(jìn)一步求出∠
=∠BCD對結(jié)論②進(jìn)行判斷,再者進(jìn)一步求出∠![]() 的度數(shù),由此判斷結(jié)論③,最后過點D作DM⊥
的度數(shù),由此判斷結(jié)論③,最后過點D作DM⊥![]() ,通過證明△ABD~△
,通過證明△ABD~△![]() ,利用相似三角形性質(zhì)進(jìn)一步分析結(jié)論⑤,據(jù)此即可得出答案.
,利用相似三角形性質(zhì)進(jìn)一步分析結(jié)論⑤,據(jù)此即可得出答案.
由旋轉(zhuǎn)性質(zhì)可知:![]() ,
,
∴![]() 為等腰三角形,即①正確;
為等腰三角形,即①正確;
∵∠ACB=30°,
∴∠![]() =∠
=∠![]() =30°,
=30°,
又∵∠![]() =∠BAC=45°,
=∠BAC=45°,
∴∠![]() =75°,
=75°,
∴∠![]() =180°75°30°=75°,
=180°75°30°=75°,
∴CA=![]() ,即④正確;
,即④正確;
∵∠BAC=45°,
∴∠![]() =45°+75°=120°,
=45°+75°=120°,
∵![]() =AB,
=AB,
∴∠![]() =∠ABD=30°,
=∠ABD=30°,
在△![]() 與△BCD中,
與△BCD中,
∵∠![]() =∠BDC,∠
=∠BDC,∠![]() =∠BCD=30°,
=∠BCD=30°,
∴△![]() ~△BCD,即②正確;
~△BCD,即②正確;
∵∠![]() =∠
=∠![]() +∠
+∠![]() =120°,
=120°,
∴旋轉(zhuǎn)角![]() ,即③錯誤;
,即③錯誤;
在△ABD與△![]() 中,
中,
∵∠ABD=∠![]() ,∠ADB=∠
,∠ADB=∠![]() ,
,
∴△ABD~△![]() ,
,
∴![]() ,
,
如圖,過點D作DM⊥![]() ,
,
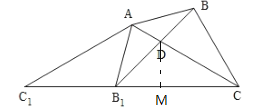
設(shè)DM=![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴AC=![]() ,
,
∴AD=![]() ,
,
∴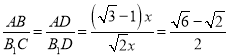 ,即⑤正確;
,即⑤正確;
綜上所述,共4個正確,
故選:C.


 海淀課時新作業(yè)金榜卷系列答案
海淀課時新作業(yè)金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標(biāo)準(zhǔn)練系列答案
輕松課堂標(biāo)準(zhǔn)練系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】![]() 年我國個人所得稅征收辦法最新規(guī)定:月收入不超過
年我國個人所得稅征收辦法最新規(guī)定:月收入不超過![]() 元的部分不收稅;月收入超過
元的部分不收稅;月收入超過![]() 元但不超過
元但不超過![]() 元的部分征收
元的部分征收![]() 的所得稅;月收入超過
的所得稅;月收入超過![]() 元但不超過
元但不超過![]() 元的部分征收
元的部分征收![]() 的所得稅
的所得稅![]() 國家特別規(guī)定月收入指個人工資收入扣除專項附加費后的實際收入(專項附加費就是子女教育費用、住房貸款利息費用、租房的租金、贍養(yǎng)老人、大病醫(yī)療費用等費用).如某人月工資收入
國家特別規(guī)定月收入指個人工資收入扣除專項附加費后的實際收入(專項附加費就是子女教育費用、住房貸款利息費用、租房的租金、贍養(yǎng)老人、大病醫(yī)療費用等費用).如某人月工資收入![]() 元,專項附加費支出
元,專項附加費支出![]() 元,他應(yīng)繳納個人所得稅為:
元,他應(yīng)繳納個人所得稅為:![]() (元).
(元).
(1)當(dāng)月收入超過![]() 元而又不超過
元而又不超過![]() 元時,寫出應(yīng)繳納個人所得稅
元時,寫出應(yīng)繳納個人所得稅![]() (元)與月收入
(元)與月收入![]() (元)之間的關(guān)系式;
(元)之間的關(guān)系式;
(2)如果某人當(dāng)月專項附加費支出![]() 元,繳納個人所得稅
元,繳納個人所得稅![]() 元,那么此人本月工資是多少元?
元,那么此人本月工資是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校根據(jù)學(xué)校實際,決定開設(shè)![]() :籃球、
:籃球、![]() :乒乓球、
:乒乓球、![]() :聲樂、
:聲樂、![]() :健美操四種活動項目(必選且只能選一個),為了解學(xué)生最喜歡哪一種活動項目,隨機抽取了部分學(xué)生進(jìn)行調(diào)查,并將調(diào)查結(jié)果整理后會制成如圖所示的不完整的統(tǒng)計圖.請你根據(jù)圖中提供的信息回答下列問題:
:健美操四種活動項目(必選且只能選一個),為了解學(xué)生最喜歡哪一種活動項目,隨機抽取了部分學(xué)生進(jìn)行調(diào)查,并將調(diào)查結(jié)果整理后會制成如圖所示的不完整的統(tǒng)計圖.請你根據(jù)圖中提供的信息回答下列問題:
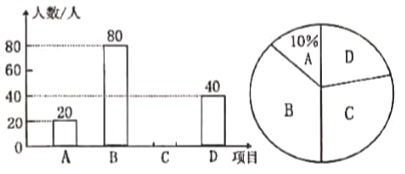
(1)求這次被調(diào)查的學(xué)生共有多少人;
(2)通過計算補全條形統(tǒng)計圖;
(3)已知該校有學(xué)生1600人,請根據(jù)調(diào)查結(jié)果估計該校最喜歡乒乓球的學(xué)生人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,線段AC=n+1(其中n為正整數(shù)),點B在線段AC上,在線段AC同側(cè)作正方形ABMN及正方形BCEF,連接AM、ME、EA得到△AME.當(dāng)AB=1時,△AME的面積記為S1;當(dāng)AB=2時,△AME的面積記為S2;當(dāng)AB=3時,△AME的面積記為
S3;則S3﹣S2= .
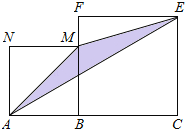
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某新建成學(xué)校舉行美化綠化校園活動,九年級計劃購買![]() ,
,![]() 兩種花木共100棵綠化操場,其中
兩種花木共100棵綠化操場,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若購進(jìn)![]() ,
,![]() 兩種花木剛好用去8000元,則購買了
兩種花木剛好用去8000元,則購買了![]() 兩種花木各多少棵?
兩種花木各多少棵?
(2)如果購買![]() 花木的數(shù)量不少于
花木的數(shù)量不少于![]() 花木的數(shù)量,請設(shè)計一種購買方案使所需總費用最低,并求出該購買方案所需總費用?
花木的數(shù)量,請設(shè)計一種購買方案使所需總費用最低,并求出該購買方案所需總費用?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:如圖1,對于直線![]() 同側(cè)的
同側(cè)的![]() 、
、![]() 兩點,若在
兩點,若在![]() 上的點
上的點![]() 滿足
滿足![]() ,則稱
,則稱![]() 為
為![]() 、
、![]() 兩點在
兩點在![]() 上的反射點,
上的反射點,![]() 與
與![]() 的和稱為
的和稱為![]() 、
、![]() 兩點的反射距離.
兩點的反射距離.

(1)如圖2,在邊長為2的正方形![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 、
、![]() 兩點在直線
兩點在直線![]() 上的反射點,求
上的反射點,求![]() 、
、![]() 兩點的反射距離;
兩點的反射距離;
(2)如圖3,![]() 內(nèi)接于
內(nèi)接于![]() ,直徑
,直徑![]() 為4,
為4,![]() ,點
,點![]() 為劣弧
為劣弧![]() 上一動點,點
上一動點,點![]() 為
為![]() 、
、![]() 兩點在
兩點在![]() 上的反射點,當(dāng)
上的反射點,當(dāng)![]() 、
、![]() 兩點的反射距離最大時,求劣弧
兩點的反射距離最大時,求劣弧![]() 的長;
的長;
(3)如圖4,在平面直角坐標(biāo)系中,拋物線![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,頂點為
,頂點為![]() ,若點
,若點![]() 為點
為點![]() 、
、![]() 在
在![]() 上的反射點,同時點
上的反射點,同時點![]() 為點
為點![]() 、
、![]() 在
在![]() 上的反射點.
上的反射點.
①請判斷線段![]() 和
和![]() 的位置關(guān)系,并給出證明;
的位置關(guān)系,并給出證明;
②求![]() 、
、![]() 兩點的反射距離與
兩點的反射距離與![]() 、
、![]() 兩點的反射距離的比值.
兩點的反射距離的比值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點A,B,C均在坐標(biāo)軸上,AO=BO=CO=1,過A,O,C作⊙D,E是⊙D上任意一點,連結(jié)CE, BE,則![]() 的最大值是( )
的最大值是( )

A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
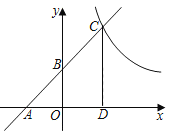
【題目】如圖,已知一次函數(shù)y=kx+b(k≠0)的圖象與x軸、y軸分別交于點A、B兩點,且與反比例函數(shù)y=![]() 的圖象在第一象限內(nèi)的部分交于點C,CD垂直于x軸于點D,其中OA=OB=OD=2.
的圖象在第一象限內(nèi)的部分交于點C,CD垂直于x軸于點D,其中OA=OB=OD=2.
(1)直接寫出點A、C的坐標(biāo);
(2)求這兩個函數(shù)的表達(dá)式;
(3)若點P在y軸上,且S△ACP=14,求點P的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com