
【題目】如圖,在四邊形ABCD中,AD∥BC,∠ABC=90°,E是AB上一點,且DE⊥CE.若AD=1,BC=2,CD=3,則CE與DE的數量關系正確的是( )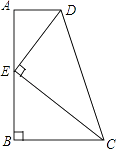
A.CE= ![]() DE
DE
B.CE= ![]() DE
DE
C.CE=3DE
D.CE=2DE
【答案】B
【解析】解:過點D作DH⊥BC,
∵AD=1,BC=2,
∴CH=1,
DH=AB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AD∥BC,∠ABC=90°,
∴∠A=90°,
∵DE⊥CE,
∴∠AED+∠BEC=90°,
∵∠AED+∠ADE=90°,
∴∠ADE=∠BEC,
∴△ADE∽△BEC,
∴ ![]() ,
,
設BE=x,則AE=2 ![]() ,
,
即 ![]() ,
,
解得x= ![]() ,
,
∴ ![]() ,
,
∴CE= ![]() DE,
DE,
故選B.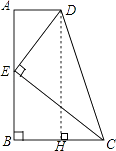
過點D作DH⊥BC,利用勾股定理可得AB的長,利用相似三角形的判定定理可得△ADE∽△BEC,設BE=x,由相似三角形的性質可解得x,易得CE,DE 的關系.本題主要考查了相似三角形的性質及判定,構建直角三角形,利用方程思想是解答此題的關鍵.


科目:初中數學 來源: 題型:
【題目】歷史上的數學巨人歐拉最先把關于![]() 的多項式用記號
的多項式用記號![]() 的形式來表示(
的形式來表示(![]() 可用其它字母,但不同的字母表示不同的多項式),例如
可用其它字母,但不同的字母表示不同的多項式),例如![]() ,把
,把![]() =某數時的多項式的值用
=某數時的多項式的值用![]() 來表示.
來表示.
例如![]() 時多項式
時多項式![]() 的值記為
的值記為![]() ,
,
已知![]() ,
,![]()
(1)求![]() 的值
的值
(2)若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=x+m的圖象與反比例函數y=![]() 的圖象交于A,B兩點,且與x軸交于點C,點A的坐標為(2,1).
的圖象交于A,B兩點,且與x軸交于點C,點A的坐標為(2,1).
(1)求m及k的值;
(2)求點C的坐標,并結合圖象寫出不等式組0<x+m≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
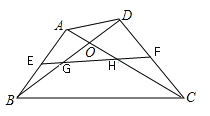
【題目】如圖,在四邊形ABCD中,對角線AC、BD相交于點O,且AC=BD,E、F分別相交是AB、CD的中點,EF分別交BD、AC于點G、H。求證:OG=OH。
查看答案和解析>>
科目:初中數學 來源: 題型:
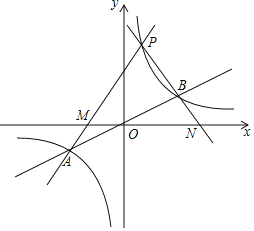
【題目】如圖,函數![]() 與
與![]() 圖象的交于點A,
圖象的交于點A,![]() 若點A的坐標為
若點A的坐標為![]() .
.
![]() 點B的坐標為______;
點B的坐標為______;
![]() 若點P為第一象限內雙曲線上不同于點B的任意一點.
若點P為第一象限內雙曲線上不同于點B的任意一點.
![]() 設直線PA交x軸于點M,直線PB交x軸于點N,求證
設直線PA交x軸于點M,直線PB交x軸于點N,求證![]() ;
;
![]() 當P的坐標為
當P的坐標為![]() 時,連結PO延長交
時,連結PO延長交![]() 于C,求證四邊形PACB為矩形.
于C,求證四邊形PACB為矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,直線
,直線![]() 與雙曲線
與雙曲線![]() 相交于點
相交于點![]() 、
、![]() ,與x軸相交于C點.
,與x軸相交于C點.
![]() 求點A、B的坐標及直線
求點A、B的坐標及直線![]() 的解析式;
的解析式;
![]() 求
求![]() 的面積;
的面積;
![]() 觀察第一象限的圖象,直接寫出不等式
觀察第一象限的圖象,直接寫出不等式![]() 的解集;
的解集;
![]() 如圖
如圖![]() ,在x軸上是否存在點P,使得
,在x軸上是否存在點P,使得![]() 的和最小?若存在,請說明理由并求出P點坐標.
的和最小?若存在,請說明理由并求出P點坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為2的正三角形ABC中,P0是BC邊的中點,一束光線自P0發出射到AC上的點P1后,依次反射到AB、BC上的點P2和P3(反射角等于入射角). 
(1)若∠P2P3B=45°,CP1=;
(2)若 ![]() <BP3<
<BP3< ![]() ,則P1C長的取值范圍是 .
,則P1C長的取值范圍是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com