【題目】已知關于x的方程x2﹣（2k﹣3）x+k2+1=0．
（1）當k為何值時，此方程有實數根；
（2）若此方程的兩個實數根x1、x2滿足|x1|+|x2|=3，求k的值．
【答案】（1）當k≤
時，此方程有實數根；（2）k的值為0．
【解析】
試題分析：（1）根據判別式的意義得到△=（2k﹣3）2﹣4（k2+1）≥0，然后解不等式即可；
（2）根據根與系數的關系得到x1+x2=2k﹣3，x1x2=k2+1＞0，則可判斷x1、x2同號，然后去絕對值，當x1+x2=3，即2k﹣3=3；當﹣（x1+x2）=3，即﹣（2k﹣3）=3，然后分別解關于k的方程即可．
解：（1）若方程有實數根，
則△=（2k﹣3）2﹣4（k2+1）≥0，
∴k≤
∴當k≤時，此方程有實數根；
（2）根據題意得x1+x2=2k﹣3，x1x2=k2+1＞0，
則x1、x2同號，
當x1＞0，x2＞0，則x1+x2=3，即2k﹣3=3，解得k=3，
當k=3時，原方程無實數根，舍去，
當x1＜0，x2＜0，則﹣（x1+x2）=3，即﹣（2k﹣3）=3，解得k=0，
即k的值為0．
科目：初中數學 來源： 題型：
【題目】小軍同學在學校組織的社會實踐活動中，負責了解他所居住的小區450戶居民的生活用水情況，他從中隨機調查了50戶居民的月均用水量（單位：t）,并繪制了樣本的頻數分布表：
月 均 用水量 |
|
|
|
|
|
|
|
頻數 | 2 | 12 | ① | 10 | ② | 3 | 2 |
百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
（1）請根據題中已有的信息補全頻數分布表：① ，② ，③ ；
（2）如果家庭月均用水量“大于或等于5t且小于8t”為中等用水量家庭，請你通過樣本估計總體中的中等用水量家庭大約有多少戶？
（3）記月均用水量在
范圍內的兩戶為
、
，在
范圍內3戶為
、
、
，從這5戶家庭中任意抽取2戶，試完成下表，并求出抽取的2戶家庭來自不同范圍的概率.
|
|
|
|
| |
| |||||
| |||||
| |||||
| |||||
|
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】填空:
（1）乘積是1的兩個數互為______;
（2）有理數的除法法則，除以一個數等于乘以這個數的______;
（3）兩數相除，同號得______，異號得______，并把絕對值______，0除以任何一個不等于0的數都得______.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有一種“算24”的游戲，其規則是：任取四個1～13之間的自然數，將這四個數（每數只能用一次）進行加減乘除混合運算，其結果為24.例如2，3，4，5作運算.（5+3－2）×4=24，現有四個有理數3、4、－6、10，運用以上規則寫出等于24的算式，你能寫出幾種算法?
查看答案和解析>>
科目：初中數學 來源： 題型：
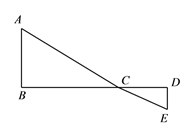
【題目】如圖， 
為線段
上一動點，分別過點
、
作
， 
，連接
、
，已知
， 
， 
，設
．
（1）用含
的代數式表示
的長；
（2）請問點
在什么位置時， 
的值最小，求出這個最小值；
（3）根據（2）中的規律和結論，構圖求出代數式
的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】《算法統宗》記載古人丈量田地的詩：“昨日丈量地回，記得長步整三十．廣斜相并五十步，不知幾畝及分厘．”其大意是：昨天丈量了田地回到家，記得長方形田的長為30步，寬和對角線之和為50步．不知該田有幾畝？請我幫他算一算，該田有___畝（1畝＝240平方步）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
